A menudo, cuando se aplica el concepto predicción en el sector eléctrico tiende a relacionarse inmediatamente con dos conceptos: el consumo y el precio. El primero el fundamental para no penalizar desvíos. El segundo, tiene más que ver con el trading puro y duro.
Ambos, eso sí, son fundamentales para optimizar el gross margin de la compañía, y más aún cuando cuando se empieza en pequeñas comercializadoras, donde aún no existen equipos de big data que puedan desarrollar los algoritmos de predicción correspondientes. En multitud de ocasiones, el analista se ve abocado a trabajar en Excel algún tipo de regresión, y no es raro acabar con una ecuación de grado 7 que poco o nada tiene de validez una vez las condiciones de partida cambian.
En el sector se tiene a REE, que como operador del sistema proporciona sus propias predicciones de consumo o demanda del sistema peninsular. Es especialmente útil si la curva de la comercializadora se parece a la del sistema, y completamente inútil si el portfolio es, por ejemplo, industrial. Esto es debido a que los comportamientos varían por distintas condiciones, y ello hace más compleja su predicción.
En una serie de posts, trataré de predecir el consumo de dos curvas con diferentes técnicas y algoritmos: la propia del sistema, y la de una vivienda unifamiliar.
Predicción de la curva de REE mediante random forest
Me centraré en la predicción de la curva de REE. Idóneamente sería óptimo predecir la curva horaria, pero por razones de disponibilidad de otros datos, me centraré en la predicción diaria. En primer lugar, llamaré a la API de ESIOS (REE) para obtener todos los datos históricos de previsión de demanda (ojo, no de la demanda programada). Aquí explicaba cómo hacerlo.
library(RCurl)
library(dplyr)
library(lubridate)
library(jsonlite)
library(tidyr)El indicador previsión de la demanda se corresponde con el id = 460.
# Definición del ID del indicador
indicador <- 460
# Token
httpheader <- 'Authorization: Token token="cd1ef004d4b59456a62610af711340aebc1555e30c4bf656640326358c92341b"'
# Hasta qué fecha fin quiero los datos
hoy <- ymd_hms(paste0(Sys.Date(), " 00:00:00" ), tz = "Europe/Madrid")
# URL
uri <- paste0("https://api.esios.ree.es/indicators/", indicador, "?start_date=", "01-01-2014", "T", "00:00:00+02:00&end_date=", as.Date(hoy), "T", "23:50:00+02:00&geo_agg=sum&geo_ids&time_trunc=hour&time_agg=&locale=es")# Extracción del JSON
extraccion <- getURI(uri, httpheader = httpheader)
extraccion <- fromJSON(txt=extraccion)
# Limpieza de la tabla
prevision_demanda <- extraccion %>%
as.data.frame() %>%
select(indicator.values.tz_time, indicator.values.value) %>%
rename(datetime = indicator.values.tz_time,
prevision_demanda = indicator.values.value)
# Corrección de la fecha para tenerla en hora local peninsular
prevision_demanda$datetime <- ymd_hms(prevision_demanda$datetime, tz = "Europe/Madrid", locale = Sys.getlocale("LC_TIME"))
# Muestra
head(prevision_demanda)## datetime prevision_demanda
## 1 2014-01-01 00:00:00 26252
## 2 2014-01-01 01:00:00 24040
## 3 2014-01-01 02:00:00 22829
## 4 2014-01-01 03:00:00 21816
## 5 2014-01-01 04:00:00 21439
## 6 2014-01-01 05:00:00 21938Inclusión de variables exógenas
El dataset inicial es bastante pobre, aunque sea la materia prima con la que trabajar. A priori, se sabe que la demanda del sistema es función de la laboralidad, la temperatura y además tiene un efecto curva.
Para incluir la laboralidad basta con crear en Excel un archivo .csv identificando qué días son festivos nacionales (podría afinar mucho más indicando otros festivos regionales). Al día festivo le asignaré el código F.
# Cargo festivos
festivos <- read.csv2("/Users/pherreraariza/Documents/ModeloESIOS/calendario/festivos.csv", colClasses = c("character", "factor"))
festivos$fecha <- as.Date(festivos$fecha, "%d-%m-%Y")
# Inclusión de festivos en el dataset original
prevision_demanda_festivos <- prevision_demanda %>% mutate(fechadummy = as.Date(datetime, tz = "Europe/Madrid")) %>%
group_by(fechadummy) %>%
summarise(demanda_diaria = mean(prevision_demanda)) %>%
left_join(festivos, by = c("fechadummy" = "fecha"))
head(prevision_demanda_festivos)## # A tibble: 6 x 3
## fechadummy demanda_diaria tipo
## <date> <dbl> <fct>
## 1 2014-01-01 26545. F
## 2 2014-01-02 26391. <NA>
## 3 2014-01-03 28107. <NA>
## 4 2014-01-04 24900. <NA>
## 5 2014-01-05 25352. <NA>
## 6 2014-01-06 25681. FA continuación acabo de rellenar los valores vacío de tipo de día: los fines de semana serán también festivos, y el resto (es decir, descontados festivos nacionales y fines de semana), serán laborables y se les asignará el código L.
# Asignación del día de la semana para diferenciar laborables y fines de semana
prevision_demanda_dias <- prevision_demanda_festivos %>% mutate(weekday = as.factor(wday(fechadummy)),
tipo = if_else(is.na(tipo) & weekday %in% c(2,3,4,5,6), "L", "F"),
mes = month(fechadummy),
quarter = ceiling(mes/3))
head(prevision_demanda_dias)## # A tibble: 6 x 6
## fechadummy demanda_diaria tipo weekday mes quarter
## <date> <dbl> <chr> <fct> <dbl> <dbl>
## 1 2014-01-01 26545. F 4 1. 1.
## 2 2014-01-02 26391. L 5 1. 1.
## 3 2014-01-03 28107. L 6 1. 1.
## 4 2014-01-04 24900. F 7 1. 1.
## 5 2014-01-05 25352. F 1 1. 1.
## 6 2014-01-06 25681. F 2 1. 1.En cuanto a la temperatura, es realmente difícil encontrar una base de datos fiable, gratuita e integrada en algún package en R, pero una opción no excesivamente mala es utilizar los datos de Global Surface Summary of the Day (GSOD), de la NOAA. Dado que los datos son diarios, únicamente podré predecir la potencia media diaria de la demanda, y no la curva como pretendía en un primer momento.
Lo primero es obtener un inventario de los datos y estaciones con una sencilla función:
library(GSODR)##
## GSOD is distributed free by the U.S. NCEI with the
## following conditions.
## 'The following data and products may have conditions placed
## their international commercial use. They can be used within
## the U.S. or for non-commercial international activities
## without restriction. The non-U.S. data cannot be
## redistributed for commercial purposes. Re-distribution of
## these data by others must provide this same notification.
## WMO Resolution 40. NOAA Policy'
##
## GSODR does not redistribute any weather data itself. It
## only provides an interface for R users to download these
## data, however it does redistribute station metadata in the
## package.inventario <- get_inventory()##
## THIS INVENTORY SHOWS THE NUMBER OF WEATHER OBSERVATIONS BY STATION-YEAR-MONTH FOR BEGINNING OF RECORD THROUGH AUGUST 2019. THE DATABASE CONTINUES TO BE UPDATED AND ENHANCED, AND THIS INVENTORY WILL BE UPDATED ON A REGULAR BASIS.head(inventario)## # A tibble: 6 x 14
## STNID YEAR JAN FEB MAR APR MAY JUN JUL AUG SEP OCT
## <chr> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
## 1 00701… 2011 0 0 2104 2797 2543 2614 382 0 0 0
## 2 00701… 2013 0 0 0 0 0 0 710 0 0 0
## 3 00702… 2012 0 0 0 0 0 0 367 0 0 0
## 4 00702… 2014 0 0 0 0 0 0 180 0 4 0
## 5 00702… 2016 0 0 0 0 0 794 0 0 0 0
## 6 00702… 2017 0 914 2626 380 277 406 1230 1010 0 0
## # ... with 2 more variables: NOV <int>, DEC <int>Ahora miraré qué estaciones españolas tiene el inventario:
load(system.file("extdata", "country_list.rda", package = "GSODR"))
load(system.file("extdata", "isd_history.rda", package = "GSODR"))
station_locations <- left_join(isd_history, country_list, by = c("CTRY" = "FIPS"))
# create data.frame for Australia only
spain_station <- subset(station_locations, COUNTRY_NAME == "SPAIN")
head(spain_station)## # A tibble: 6 x 16
## USAF WBAN STN_NAME CTRY STATE CALL LAT LON ELEV_M BEGIN END
## <chr> <chr> <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 080010 99999 LA CORU… SP <NA> <NA> 43.4 -8.42 67.0 1.93e7 2.02e7
## 2 080020 99999 A CORUNA SP <NA> LECO 43.3 -8.38 98.5 1.97e7 2.02e7
## 3 080030 99999 MONTEVE… SP <NA> <NA> 43.5 -8.32 240. 1.97e7 2.01e7
## 4 080050 99999 EL FERR… SP <NA> <NA> 43.5 -8.23 9.00 1.97e7 2.01e7
## 5 080070 99999 CERCEDA SP <NA> <NA> 43.2 -8.53 595. 2.00e7 2.01e7
## 6 080080 99999 LUGO/RO… SP <NA> <NA> 43.1 -7.45 446. 1.97e7 2.02e7
## # ... with 5 more variables: STNID <chr>, ELEV_M_SRTM_90m <dbl>,
## # COUNTRY_NAME <chr>, iso2c <chr>, iso3c <chr>Probaré con cargar la estación de Barajas (Madrid) para ver cuántos tiene en el inventario.
inventario %>% filter(STNID == "082210-99999")## # A tibble: 55 x 14
## STNID YEAR JAN FEB MAR APR MAY JUN JUL AUG SEP OCT
## <chr> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
## 1 0822… 1931 69 61 71 37 27 41 69 63 58 49
## 2 0822… 1932 72 70 70 71 73 71 79 73 73 78
## 3 0822… 1933 81 82 87 83 85 71 74 74 73 79
## 4 0822… 1934 86 75 82 83 79 79 77 66 69 80
## 5 0822… 1935 78 73 81 67 77 67 65 73 69 77
## 6 0822… 1936 90 80 81 79 81 74 68 67 70 24
## 7 0822… 1939 0 0 0 0 0 29 42 33 0 19
## 8 0822… 1967 317 277 342 372 472 460 479 471 631 707
## 9 0822… 1973 1252 1131 1245 1207 1240 1158 1195 1207 1142 1190
## 10 0822… 1974 1188 1111 1222 1161 1249 1222 1231 1222 1191 1194
## # ... with 45 more rows, and 2 more variables: NOV <int>, DEC <int>Seleccionaré finalmente para modelizar la estación de Barajas, al ser la que más datos contiene desde 2014, pese a que tiene algún hueco.
library(ggplot2)
library(lubridate)
barajas_weather <- get_GSOD(years = c(2014, 2015, 2016, 2017, 2018), station = "082210-99999")
# Selecciono la fecha, la temperatura diaria media, máxima y mínima
barajas_temperature <- barajas_weather %>% select(YEARMODA, TEMP, MAX, MIN)
# Gráfico de las temperaturas
barajas_temperature %>% gather(Measurement, gather_cols = TEMP:MIN) %>%
ggplot(aes(x = ymd(YEARMODA), y = value, colour = Measurement)) +
geom_line() +
scale_color_brewer(type = "qual", na.value = "black") +
scale_y_continuous(name = "Temperature") +
scale_x_date(name = "Date") +
theme_bw()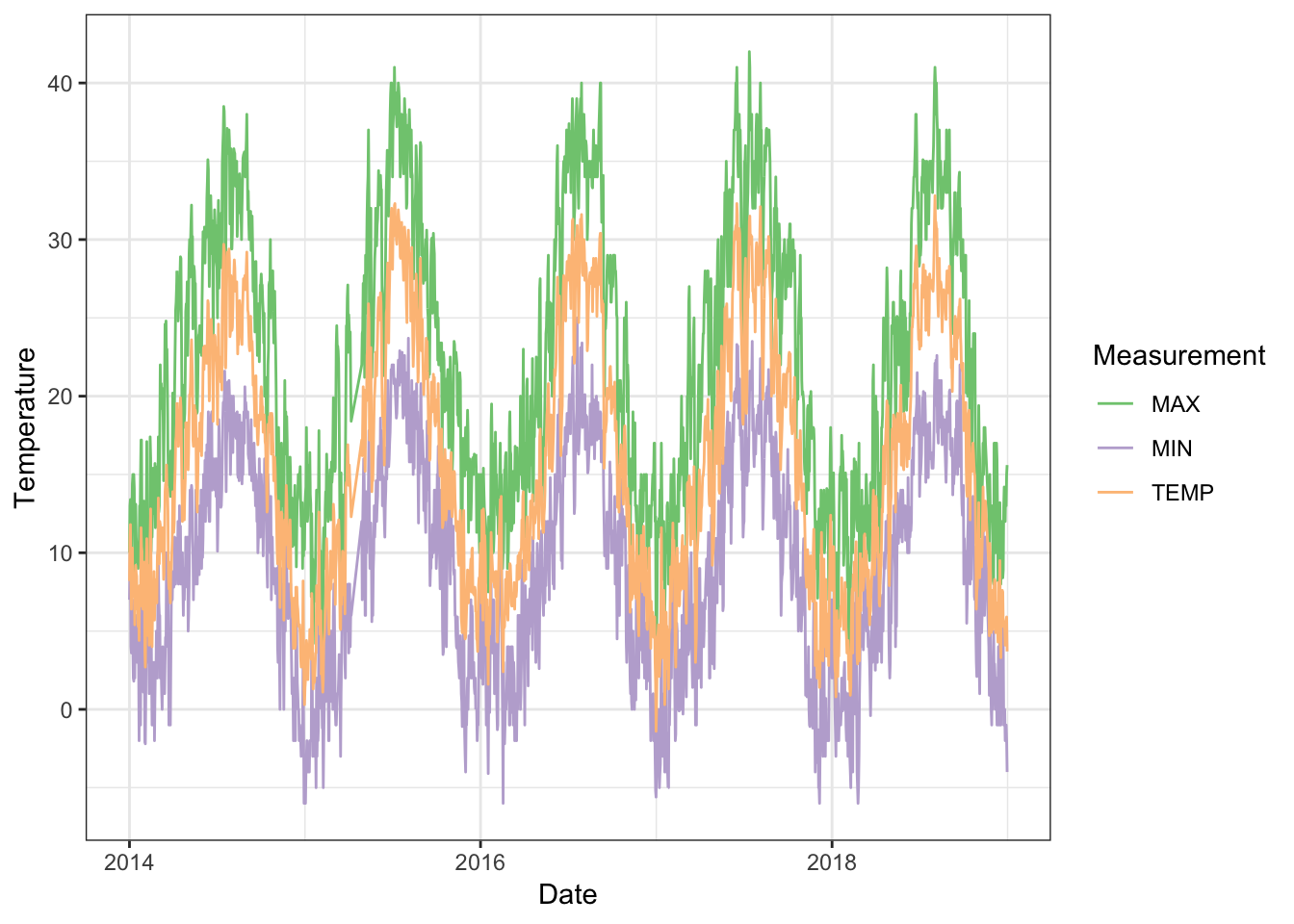
# Uno los datos al dataset original
prevision_demanda_final <- prevision_demanda_dias %>% left_join(barajas_temperature, by = c("fechadummy" = "YEARMODA"))
# Gráfico de la demanda
prevision_demanda_final %>% mutate(dia_del_año = as.numeric(format(fechadummy, "%j"))) %>%
ggplot(aes(x = dia_del_año, y = demanda_diaria, shape = as.factor(year(fechadummy)), color = as.factor(year(fechadummy)))) + geom_line() + facet_grid(as.factor(year(fechadummy)) ~ ., scales = "free_x")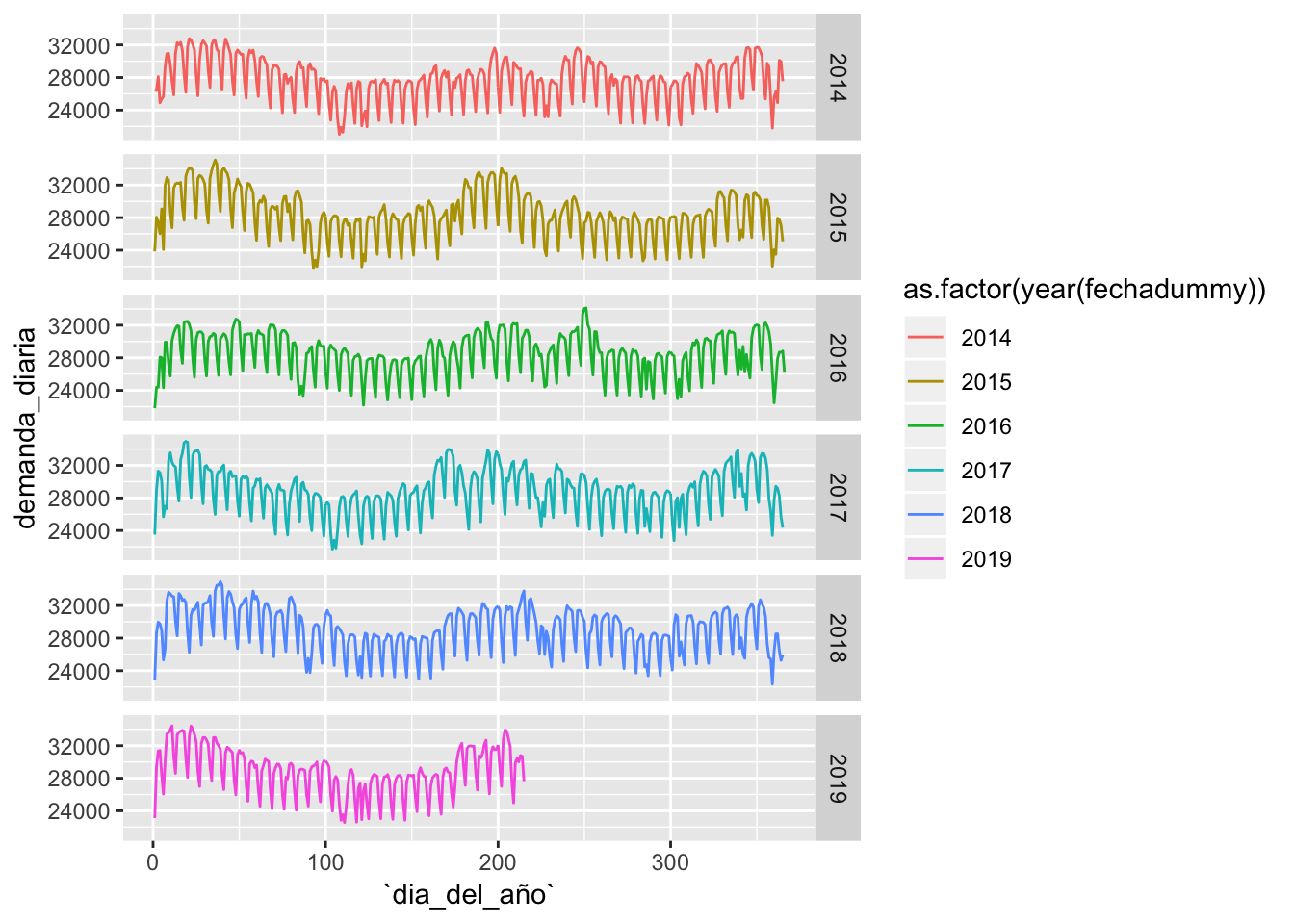
Para simplificar el modelo, he seleccionado únicamente las temperaturas media, máxima y mínima, y pese a que no es correcto utilizar sólo los datos de una estación para correlacionarla con toda la demanda peninsular, servirá para ver cómo se puede entrenar el modelo.
Correlación de variables
Intuitivamente, parece claro que no debería encontrar una altísima correlación entre temperaturas y demanda, dada la simplicidad acometida en la selección de variables, pero realizaré la correlación de Spearman para ver qué resultado se obtiene:
library(corrr)
# Correlación de variables
cor_demanda <- prevision_demanda_final %>% filter(quarter == 1) %>%
select(-fechadummy, -tipo, -weekday, -mes, -quarter) %>%
correlate(method = "spearman")##
## Correlation method: 'spearman'
## Missing treated using: 'pairwise.complete.obs'# Tabla de correlación
cor_demanda %>% fashion()## rowname demanda_diaria TEMP MAX MIN
## 1 demanda_diaria -.41 -.37 -.27
## 2 TEMP -.41 .74 .78
## 3 MAX -.37 .74 .26
## 4 MIN -.27 .78 .26# Gráfico de correlación
cor_demanda %>% network_plot()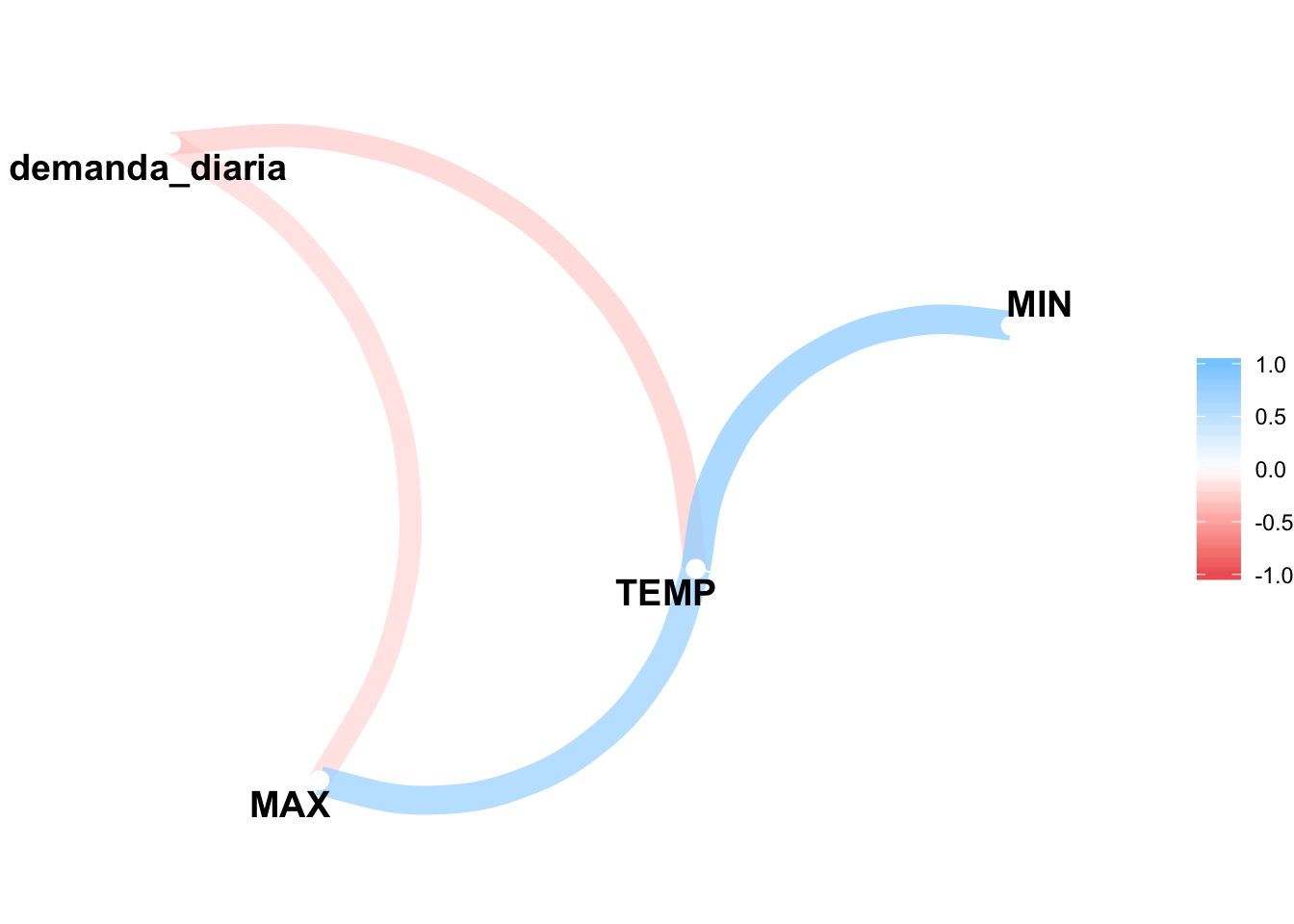
cor_demanda %>% rplot(print_cor = TRUE)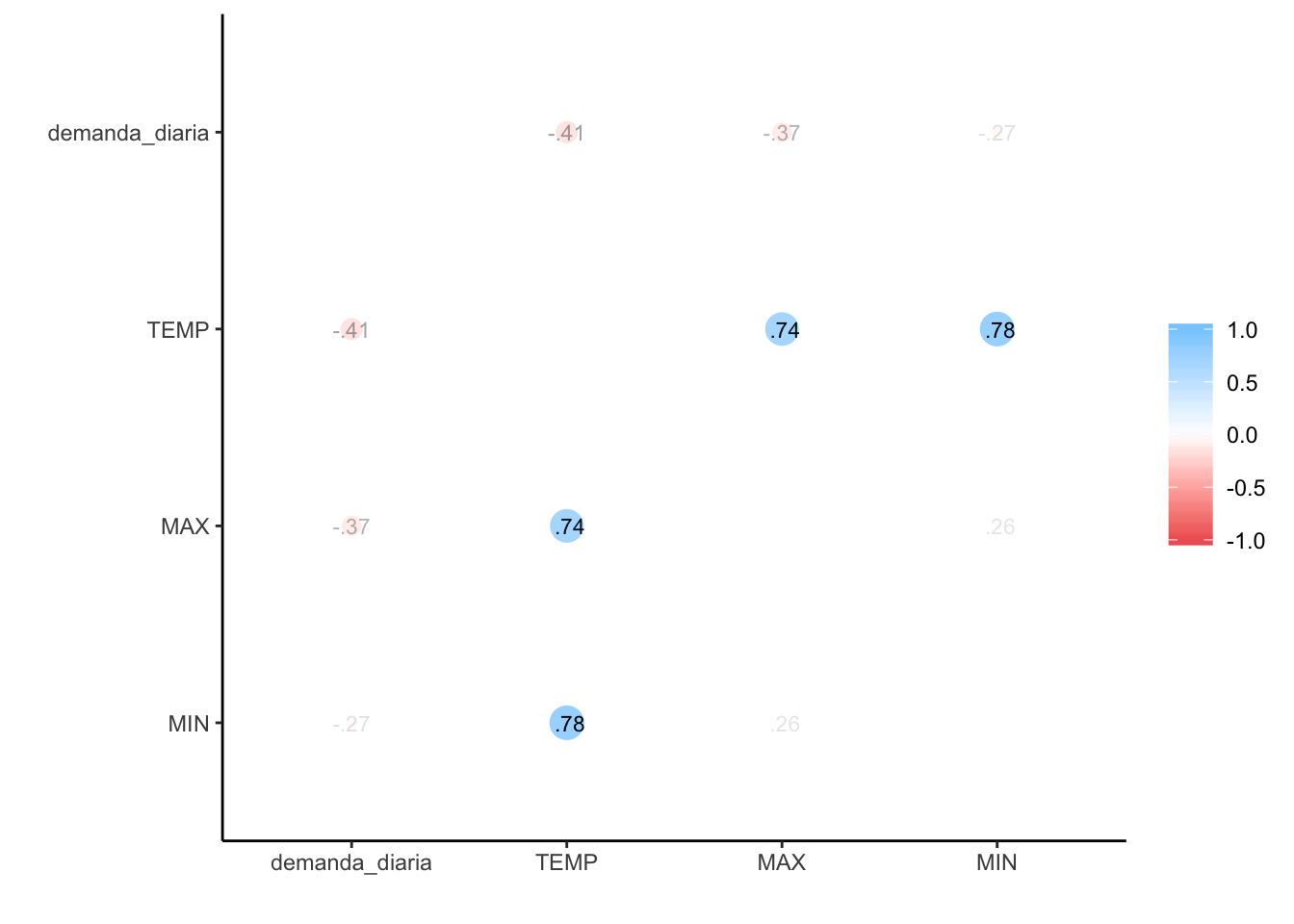
Un 41% de correlación entre demanda diaria y temperatura media no es un valor demasiado bueno, pero podría servir como punto de partida.
Creación del modelo random forest
En primer lugar, ¿por qué un random forest? Bueno, es una técnica muy popular, que consiste en crear múltiples árboles de decisión modelizados sobre un conjunto de datos aleatorios pero con misma distribución. Haciendo una analogía simple podría resumirse en el siguiente ejemplo:
Un estudiante quiere saber qué carrera estudiar para obtener un mejor salario. Le pregunta a un conocido que ya trabaja, y éste le hace diferentes preguntas para poder darle su mejor respuesta. El estudiante se basará en la respuesta para tomar una decisión. Hasta aquí sería un ejemplo de árbol de decisión. Pero ahora, nuestro estudiante pregunta a muchísimos conocidos más, de diferentes sectores y países, y una vez tiene todas las respuestas, toma una decisión. Esto es un random forest.
En este post lo explican bastante bien.
Para comenzar, es básico crear un set de entrenamiento y otro de test sobre el que validar mis predicciones. En general, se suelen tomar entre el 70-80% de los datos como set de entrenamiento y el resto como test. Utilizaré como datos de entrenamiento todos los datos diarios desde el 1 de enero de 2014 hasta el 31 de diciembre de 2017. El resto, el año acumulado de 2018 lo utilizaré como set de test para probar si el modelo es bueno. También eliminaré del conjunto de datos las fechas que les faltan el dato de temperatura, que afortunadamente no son muchos (podría imputarle la media entre los valores anteriores y posteriores, pero lo haré en otro post donde ajuste el modelo mejor):
library(caret)
library(recipes)
# Creo un set de entrenamiento y un set de testeo
set.seed(1)
trainset <- prevision_demanda_final %>% na.omit() %>% filter(fechadummy < "2018-01-01")
testset <- prevision_demanda_final %>% na.omit() %>% filter(fechadummy >= "2018-01-01")
# Especifico la validación cruzada por k-folds
control <- trainControl(method="cv", number=10, savePredictions = "final",
index=createResample(trainset$demanda_diaria, 10),
verboseIter=FALSE,
allowParallel = TRUE, predictionBounds = c(0, NA))
# Creo receta para entrenar el modelo
recipe_rf <- recipe(demanda_diaria ~ MIN + MAX + TEMP + weekday + tipo + mes + quarter, trainset) %>%
step_naomit(all_predictors()) %>%
step_dummy(all_nominal()) %>%
step_center(all_predictors()) %>%
step_scale(all_predictors())
# Entreno el modelo
model_rf <- train(recipe_rf, data = trainset, method="ranger", importance="impurity", trControl=control, metric="RMSE")
# Métricas del modelo
model_rf## Random Forest
##
## 1440 samples
## 8 predictor
##
## Recipe steps: naomit, dummy, center, scale
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 1440, 1440, 1440, 1440, 1440, 1440, ...
## Resampling results across tuning parameters:
##
## mtry splitrule RMSE Rsquared MAE
## 2 variance 1265.886 0.8067708 924.1219
## 2 extratrees 1366.333 0.7860015 1034.3257
## 7 variance 1211.962 0.8071940 859.8012
## 7 extratrees 1191.004 0.8137332 841.6375
## 12 variance 1239.597 0.7990272 882.4493
## 12 extratrees 1198.285 0.8116981 847.8041
##
## Tuning parameter 'min.node.size' was held constant at a value of 5
## RMSE was used to select the optimal model using the smallest value.
## The final values used for the model were mtry = 7, splitrule =
## extratrees and min.node.size = 5.predicciones_train <- data.frame(pred=predict(model_rf, trainset))
predicciones_train$obs <- trainset$demanda_diaria
predicciones_train$model <- model_rf$method
predicciones_train$dataType <- "Training"
predicciones_train$object <- "Object1"
# Gráfico de predicho vs observado
plotObsVsPred(predicciones_train)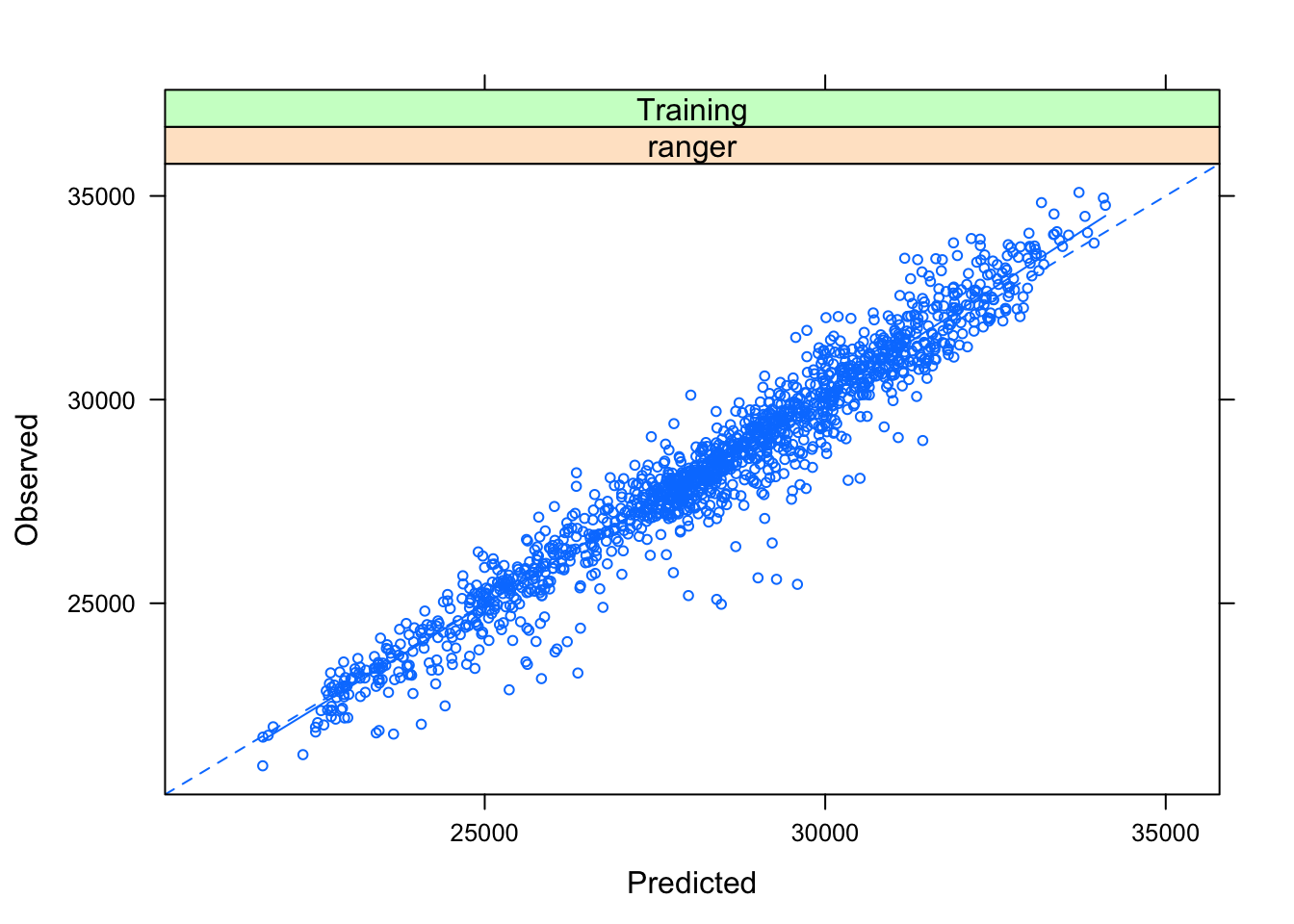
# Gráfico de residuos
ggplot(predicciones_train, aes(x=pred, y=(obs-pred))) + geom_point() + geom_smooth() + ggtitle("Random forest Train")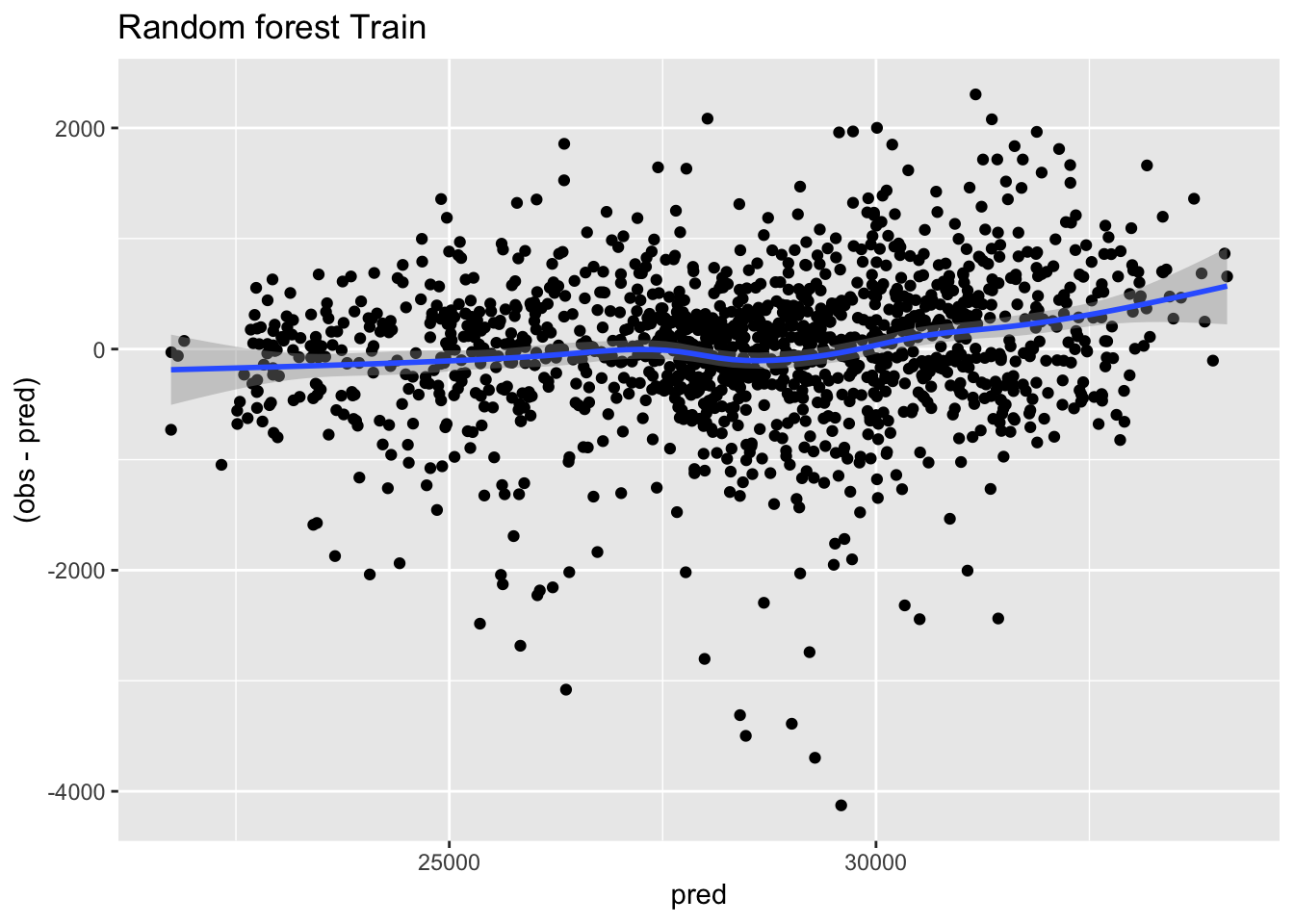
El modelo tiene un error medio absoluto (MAE) en el set de entrenamiento de aproximadamente 847 MWh (por exceso o defecto). No está mal para hacerlo con datos tan precarios y no haber hecho ninguna ingeniería de variables.
El gráfico de residuos o errores debería mostrar una nube de puntos sin patrón, centrados en el 0, pero no es así: tiene una tendencia a infraestimar el resultado cuando los valores reales son altos, señal de que al modelo le faltaría alguna variable que explicara mejor la varianza.
Aplicaré ahora el modelo para predecir el set de test (ciego totalmente a los datos de entrenamiento):
# Realizo predicción sobre el set de test
demanda_predecida <- predict(model_rf, testset)
# Cálculo de métricas
postResample(pred = demanda_predecida, obs = testset$demanda_diaria)## RMSE Rsquared MAE
## 1166.669092 0.867151 934.776709El error medio absoluto más o menos se mantiene (934 MWh), lo cual indica que no tenemos a priori problema de sobreajuste (overfitting). El R2 es del 86.7%, lo cual es un valor alto para un modelo tan rudimentario.
Graficando cómo quedan las curvas reales y las predecidas, obtendo los siguientes gráficos:
# Gráfico de predicciones vs observaciones en la serie
testset %>% cbind(demanda_predecida) %>% select(fechadummy, demanda_diaria, demanda_predecida) %>% gather(key = tipo, value = demanda, -fechadummy) %>% ggplot(aes(x = fechadummy, y = demanda, color = tipo)) + geom_line()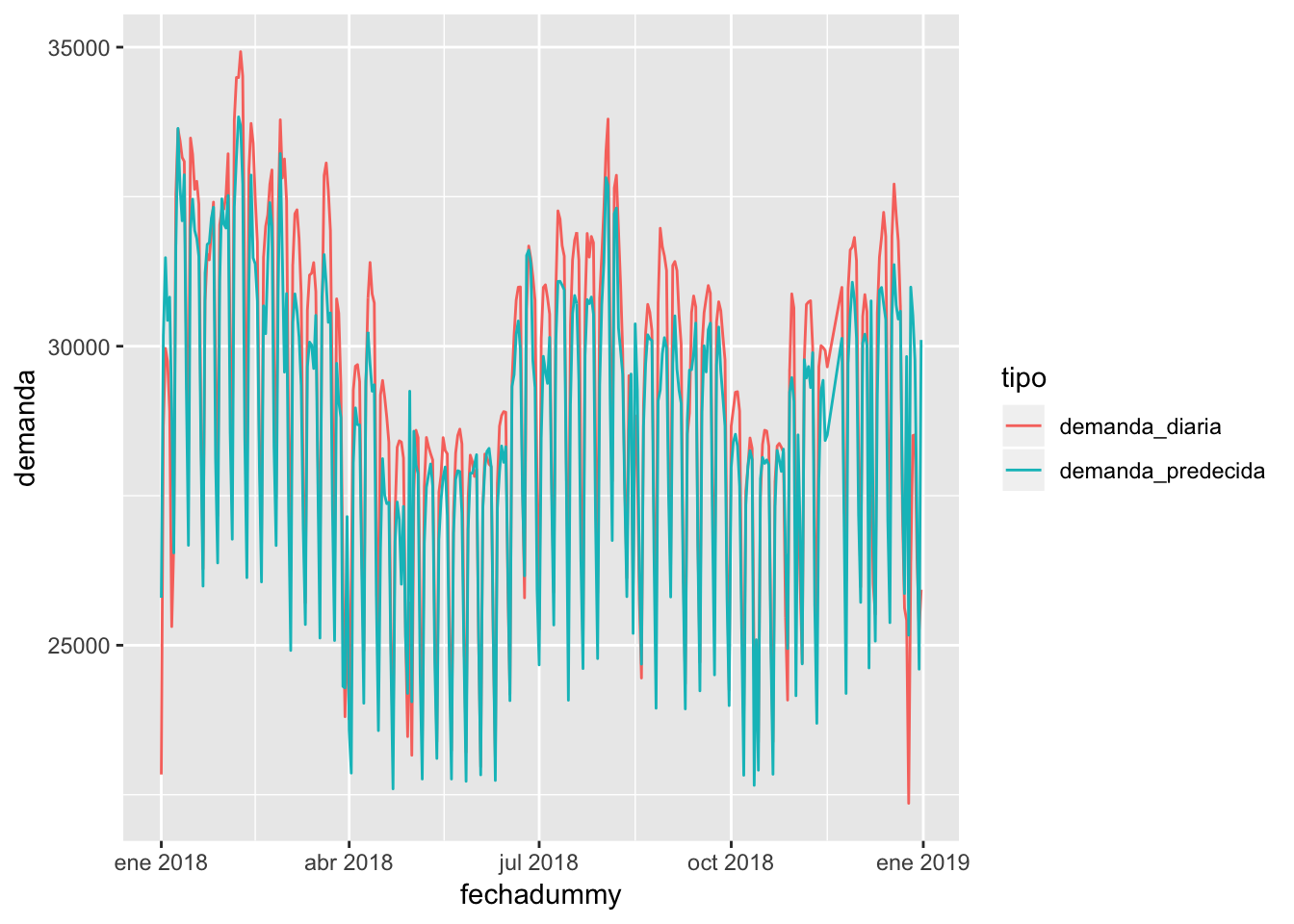
# Gráfico de predicciones vs observaciones en agosto de 2018
testset %>% cbind(demanda_predecida) %>% filter(mes == 8) %>% select(fechadummy, demanda_diaria, demanda_predecida) %>% gather(key = tipo, value = demanda, -fechadummy) %>% ggplot(aes(x = fechadummy, y = demanda, color = tipo)) + geom_line()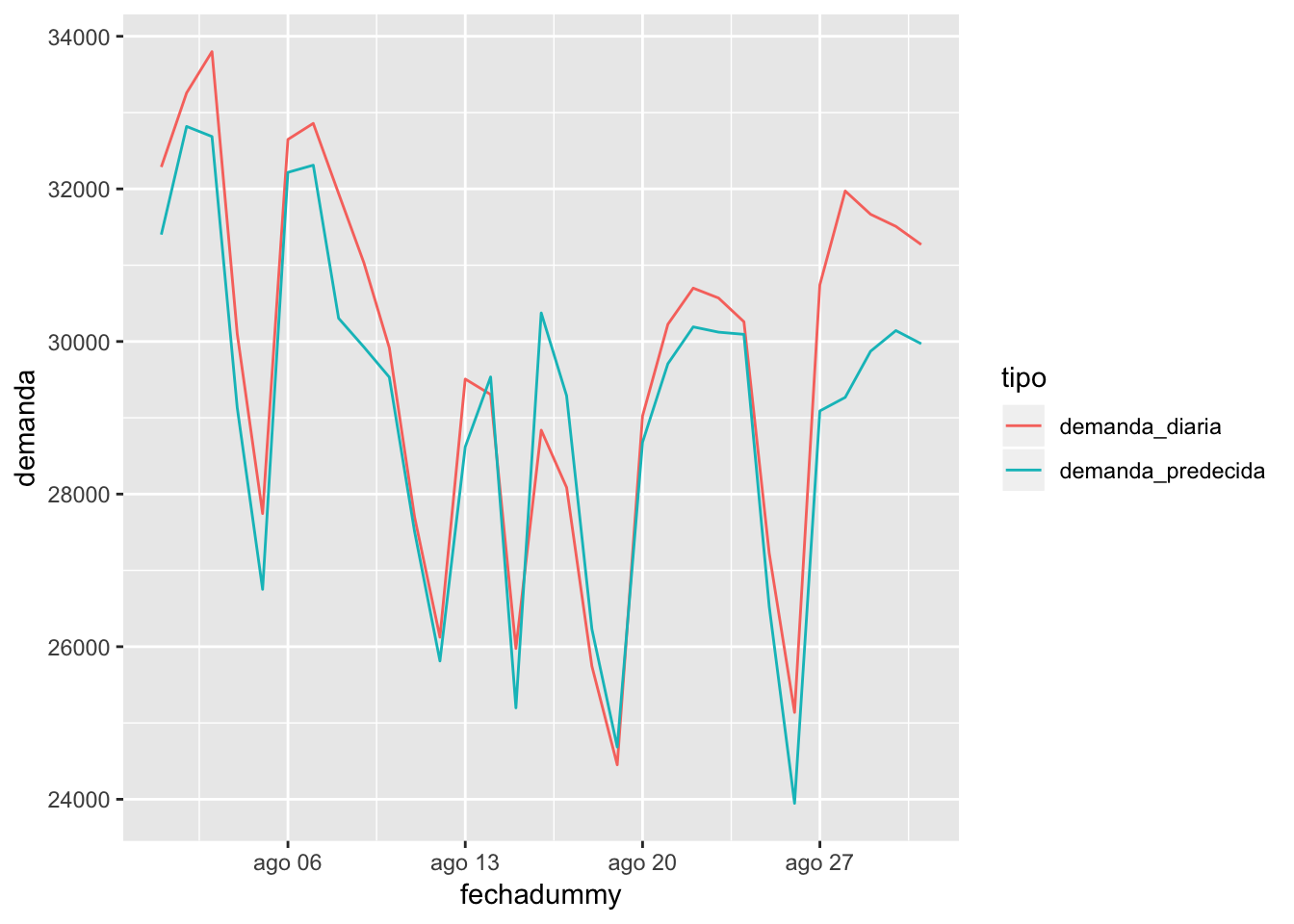
Fijándonos en el mes de agosto, no está mal. Parece que el modelo se queda bastante corto en general, pero podría mejorarlo con las siguientes operaciones:
- Encontrar valores horarios de temperatura y añadir la columna hora. Esto ajustaría la curva horaria y posiblemente el error acumulado sería menor.
- Podría probar con otros algoritmos o con ensamblajes de varios de ellos para reducir el error.
- También se podría probar con ingeniería de variables (transformaciones logarítmicas, de Box-Cox, datos laggeados, etc) para iterar y ver si mejora el error.
- Podría prescindir de los algoritmos habituales y realizar una aproximación por time series (aquí hablo de ello).