En la anterior entrada, trataba de predecir el consumo de la demanda de REE atendiendo a variables temporales y de temperatura. Debido a que ésta última sólo podía conseguirla a nivel diario, me forzaba a realizar la predicción del consumo eléctrico a nivel diario también. Esto supone claramente un problema teniendo en cuenta que el escandallo de costes y la operativa general del sistema es horaria.
Sin embargo, tras ahondar en detalle y realizar pruebas con diversos packages, he encontrado una solución que me permite trabajar a nivel horario.
Temperatura a nivel horario
Con el package riem, es posible conseguir las temperaturas históricas de diferentes localizaciones de España (y del mundo), aunque circunscritas a las estaciones meteorológicas de los aeropuertos.
Tras consultar la documentación, puedo establecer qué estación seleccionar para la recogida de datos. Pese a que lo ideal sería conseguirla de al menos 1 estación por provincia y ponderarla con el consumo anual medio nacional de cada provincia, estableceré la de Barajas como la única a considerar.
library(lubridate)##
## Attaching package: 'lubridate'## The following object is masked from 'package:base':
##
## datelibrary(dplyr)##
## Attaching package: 'dplyr'## The following objects are masked from 'package:lubridate':
##
## intersect, setdiff, union## The following objects are masked from 'package:stats':
##
## filter, lag## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, unionlibrary(ggplot2)
library(riem)
library(weathermetrics)
library(readr)
library(tidyr)
# Listado de las estaciones de aeropuertos de España
spain_airports <- riem_stations(network = "ES__ASOS")
spain_airports## # A tibble: 70 x 4
## id name lon lat
## <chr> <chr> <dbl> <dbl>
## 1 LEAB ALBACETE (CIV/MI -1.86 39.0
## 2 LERI ALCANTARILLA(SP- -1.23 38.0
## 3 LEAL ALICANTE/EL ALTE -0.558 38.3
## 4 LEAM "ALMERIA AIRPORT " -2.37 36.8
## 5 LEGA ARMILLA (CIV/MIL -3.64 37.1
## 6 GCRR ARRECIFE/LANZARO -13.6 29.0
## 7 LEAS "ASTURIAS/AVILES " -6.04 43.6
## 8 LEBL BARCELONA AIRPOR 2.07 41.3
## 9 LEBR "BARDENAS REALES " -1.47 42.2
## 10 LEBB "BILBAO/SONDICA " -2.91 43.3
## # ... with 60 more rowsLos datos de las estaciones son registrados cada media hora, por lo que descargaré los de Madrid-Barajas y los agruparé por horas para que sea coherente con el modelo:
# Busco Barajas y descargo los datos la primera vez
barajas_airpot <- filter(spain_airports, grepl("BARAJAS", name))
barajas_raw <- riem_measures(station = barajas_airpot$id, date_start = "2014 01 01")
barajas <- barajas_raw %>% group_by(datetime = floor_date(valid, "hour")) %>%
summarize(temperature = mean(tmpf)) %>%
mutate(temperature = fahrenheit.to.celsius(temperature))
barajas %>% head(10)## # A tibble: 10 x 2
## datetime temperature
## <dttm> <dbl>
## 1 2014-01-01 00:00:00 7.
## 2 2014-01-01 01:00:00 7.
## 3 2014-01-01 02:00:00 7.
## 4 2014-01-01 03:00:00 7.
## 5 2014-01-01 04:00:00 7.
## 6 2014-01-01 05:00:00 7.
## 7 2014-01-01 06:00:00 7.
## 8 2014-01-01 07:00:00 7.
## 9 2014-01-01 08:00:00 7.
## 10 2014-01-01 09:00:00 8.# Grafico
ggplot(barajas, aes(x = datetime, y = temperature)) + geom_line() + ggtitle("Temperatura en Madrid desde el 01-01-2014")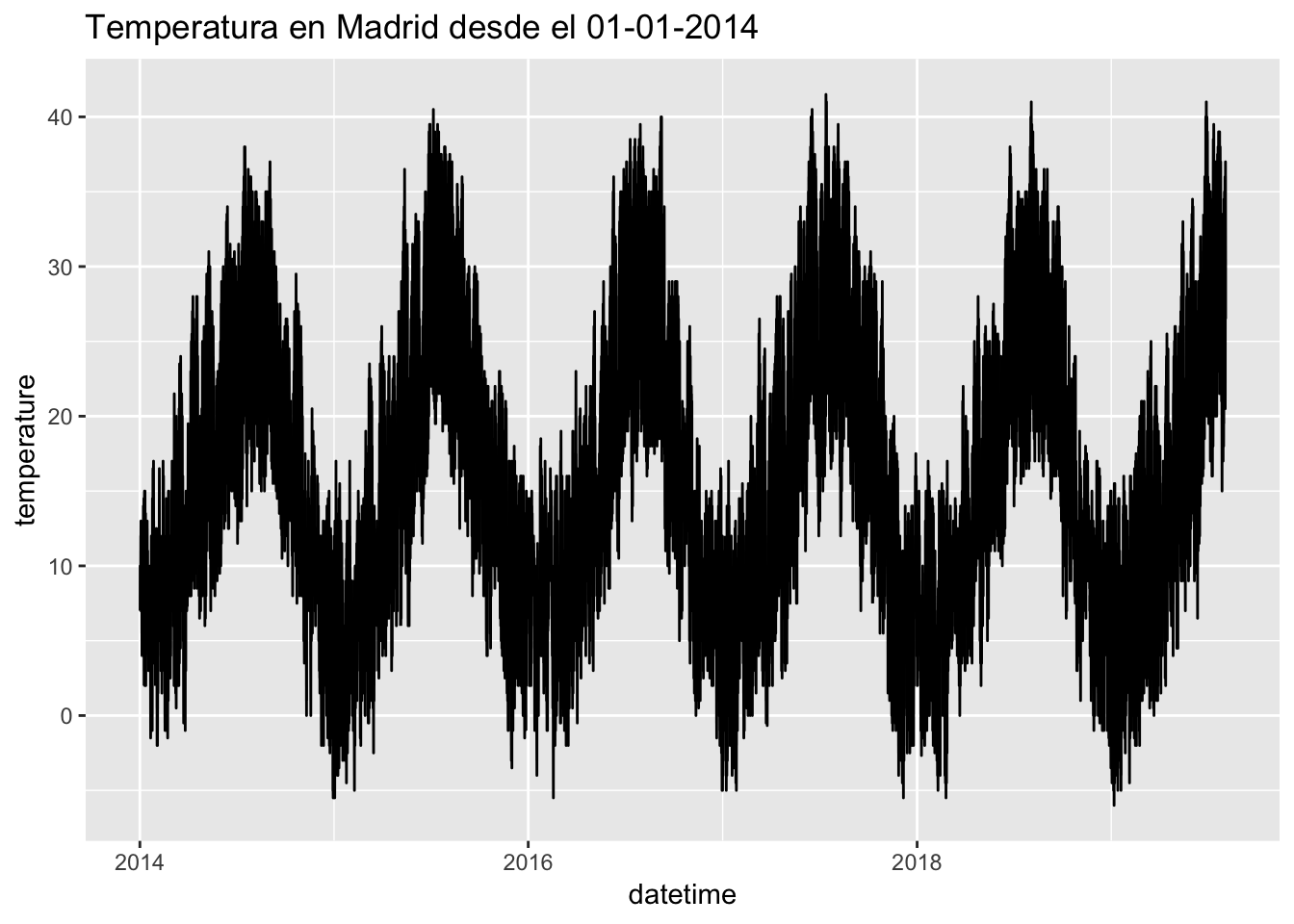
barajas %>% filter(datetime >= "2018-08-01") %>% ggplot(aes(x = datetime, y = temperature)) + geom_line() + ggtitle("Temperatura en Madrid desde el 01-01-2018")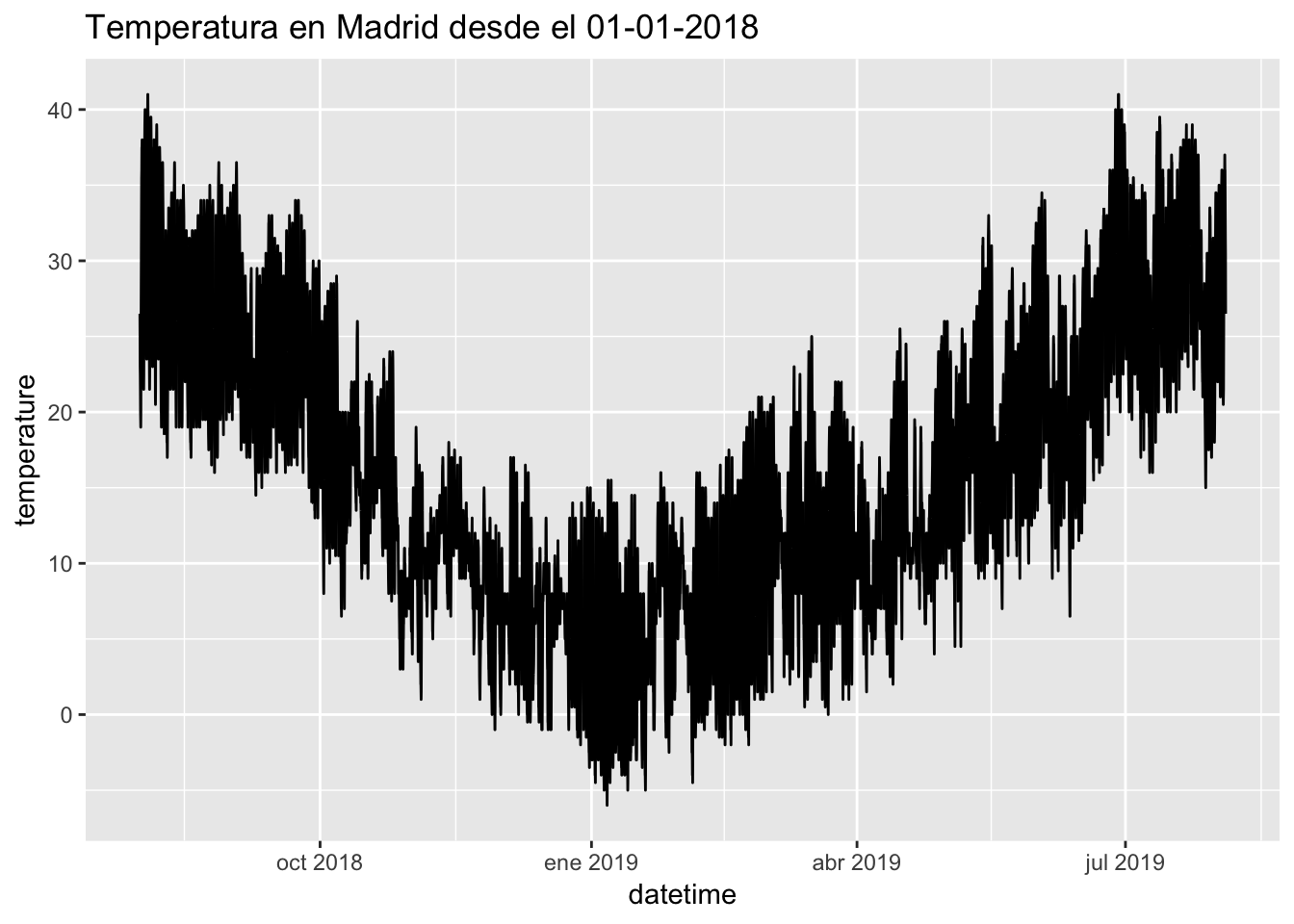
Creación del dataset
Ahora vuelvo a recuperar el indicador previsión de la demanda, que es nuestro outcome o variable a predecir, conjutnamente con las variables exógenas de laboralidad y festividades nacionales, tal y como hice en la entrada anterior:
A continuación ya sólo queda introducir los valores de temperatura:
# Join con la temperatura
prevision_demanda_horaria <- prevision_demanda_horaria %>% left_join(barajas, by = c("datetime"))
head(prevision_demanda_horaria)## datetime prevision_demanda tipo weekday mes quarter
## 1 2013-12-31 23:00:00 26252 F 4 1 1
## 2 2014-01-01 00:00:00 24040 F 4 1 1
## 3 2014-01-01 01:00:00 22829 F 4 1 1
## 4 2014-01-01 02:00:00 21816 F 4 1 1
## 5 2014-01-01 03:00:00 21439 F 4 1 1
## 6 2014-01-01 04:00:00 21938 F 4 1 1
## temperature
## 1 NA
## 2 7
## 3 7
## 4 7
## 5 7
## 6 7Entrenamiento del modelo
Entrenaré el mismo modelo, un random forest con validación cruzada para evitar en lo posible el overfitting o sobreajuste. La gran diferencia, es que las variables serán ahora horarias, y el reto es predecir la curva horaria con sólo la temperatura como variable meteorológica (en el anterior intento tenía además la mínima y la máxima diaria, además de la media).
También, utilizaré la versión lagged de la propia temperatura: esto es, correr una posición el valor horario de temperatura, para que el modelo tenga en cuanta el valor horario y el anterior, y por tanto pueda percibir los incrementos o decrementos.
library(caret)
library(recipes)
# Creo un set de entrenamiento y un set de testeo
set.seed(1)
trainset <- prevision_demanda_horaria %>% na.omit() %>% filter(datetime < "2018-01-01")
testset <- prevision_demanda_horaria %>% na.omit() %>% filter(datetime >= "2018-01-01")
# Especifico la validación cruzada por k-folds
control <- trainControl(method="cv", number=10, savePredictions = "final",
index=createResample(trainset$prevision_demanda, 10),
verboseIter=FALSE,
allowParallel = TRUE, predictionBounds = c(0, NA))
# Creo receta para entrenar el modelo
recipe_rf <- recipe(prevision_demanda ~ temperature + weekday + tipo + mes + quarter, trainset) %>%
step_lag(temperature, default = 7) %>%
step_naomit(all_predictors()) %>%
step_dummy(all_nominal()) %>%
step_center(all_predictors()) %>%
step_scale(all_predictors())
# Entreno el modelo
model_rf <- train(recipe_rf, data = trainset, method="ranger", importance="impurity", trControl=control, metric="RMSE")
# Métricas del modelo
model_rf## Random Forest
##
## 34771 samples
## 6 predictor
##
## Recipe steps: lag, naomit, dummy, center, scale
## Resampling: Cross-Validated (10 fold)
## Summary of sample sizes: 34771, 34771, 34771, 34771, 34771, 34771, ...
## Resampling results across tuning parameters:
##
## mtry splitrule RMSE Rsquared MAE
## 2 variance 3522.869 0.4209811 2893.766
## 2 extratrees 3754.523 0.3449650 3105.787
## 6 variance 3055.793 0.5522134 2285.146
## 6 extratrees 3089.786 0.5410245 2398.830
## 11 variance 3164.895 0.5293953 2316.179
## 11 extratrees 3121.789 0.5376135 2298.696
##
## Tuning parameter 'min.node.size' was held constant at a value of 5
## RMSE was used to select the optimal model using the smallest value.
## The final values used for the model were mtry = 6, splitrule =
## variance and min.node.size = 5.predicciones_train <- data.frame(pred=predict(model_rf, trainset))
predicciones_train$obs <- trainset$prevision_demanda
predicciones_train$model <- model_rf$method
predicciones_train$dataType <- "Training"
predicciones_train$object <- "Object1"
# Gráfico de predicho vs observado
plotObsVsPred(predicciones_train)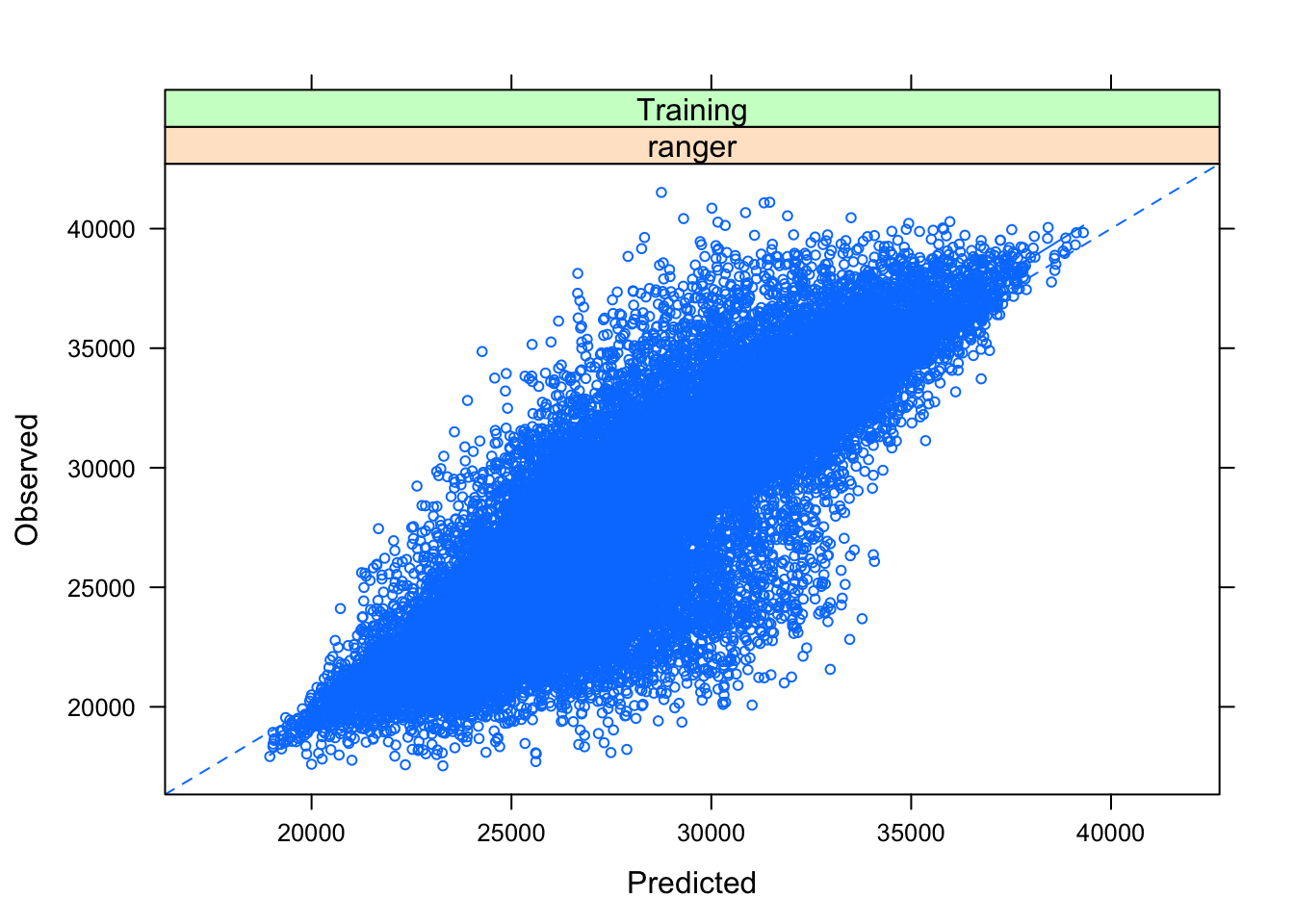
# Gráfico de residuos
ggplot(predicciones_train, aes(x=pred, y=(obs-pred))) + geom_point() + geom_smooth() + ggtitle("Random forest Train")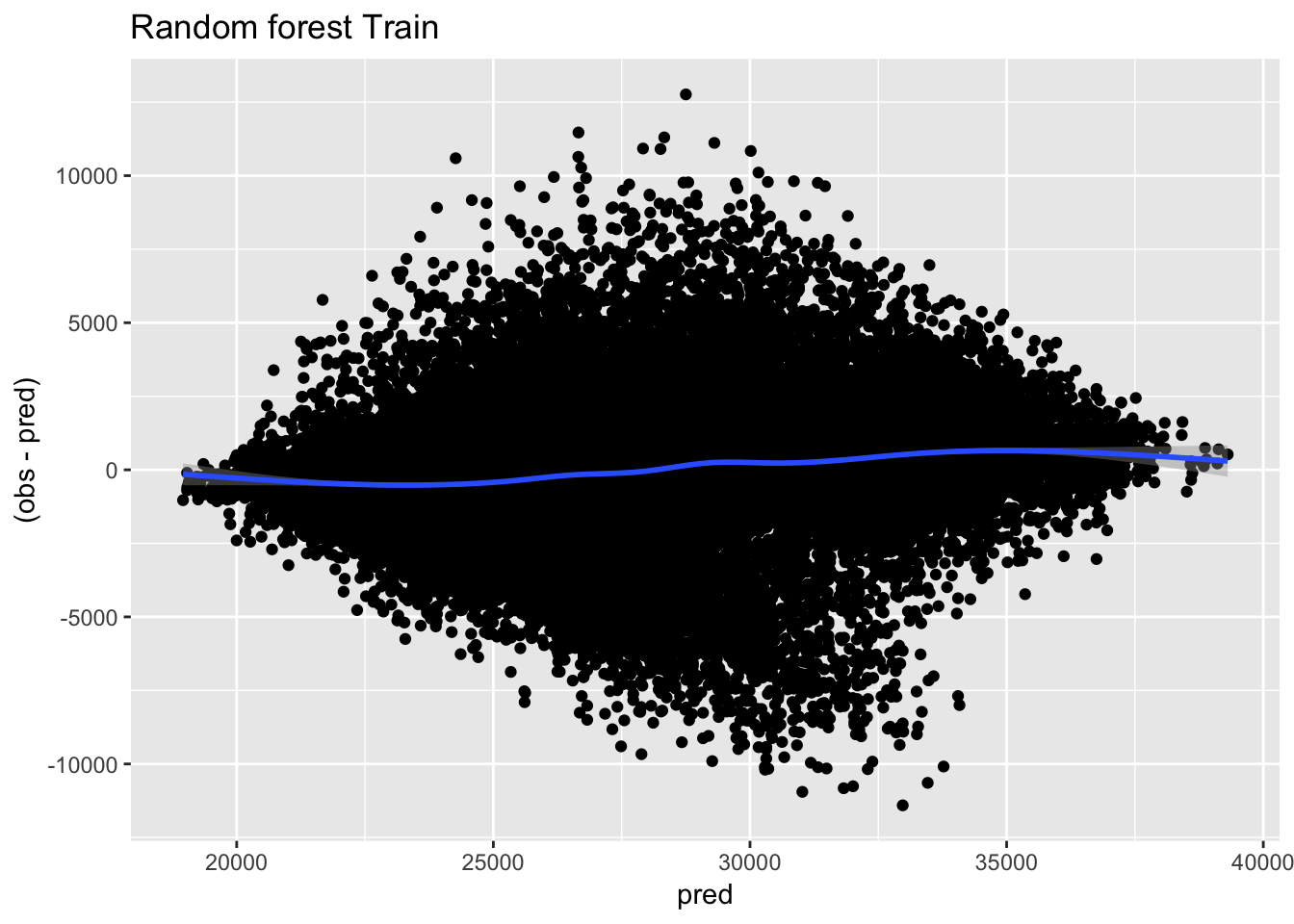
Los resultados no son buenos. Un R2 del 53.7% es bastante bajo, y el error horario absoluto medio llega a 2298 MWh, algo poco asumible para un analista. Veo ahora con el set de testeo:
# Realizo predicción sobre el set de test
demanda_predecida <- predict(model_rf, testset)
# Cálculo de métricas
postResample(pred = demanda_predecida, obs = testset$prevision_demanda)## RMSE Rsquared MAE
## 3191.6972268 0.5445554 2383.7931637Los valores se mantienen para el set de testeo, por lo que al menos, no hay problemas aparentes de overfitting.
Graficando cómo quedan las curvas reales y las predecidas, obtendo los siguientes gráficos:
# Gráfico de predicciones vs observaciones en la serie
testset %>% cbind(demanda_predecida) %>% select(datetime, prevision_demanda, demanda_predecida) %>% gather(key = tipo, value = demanda, -datetime) %>% ggplot(aes(x = datetime, y = demanda, color = tipo)) + geom_line()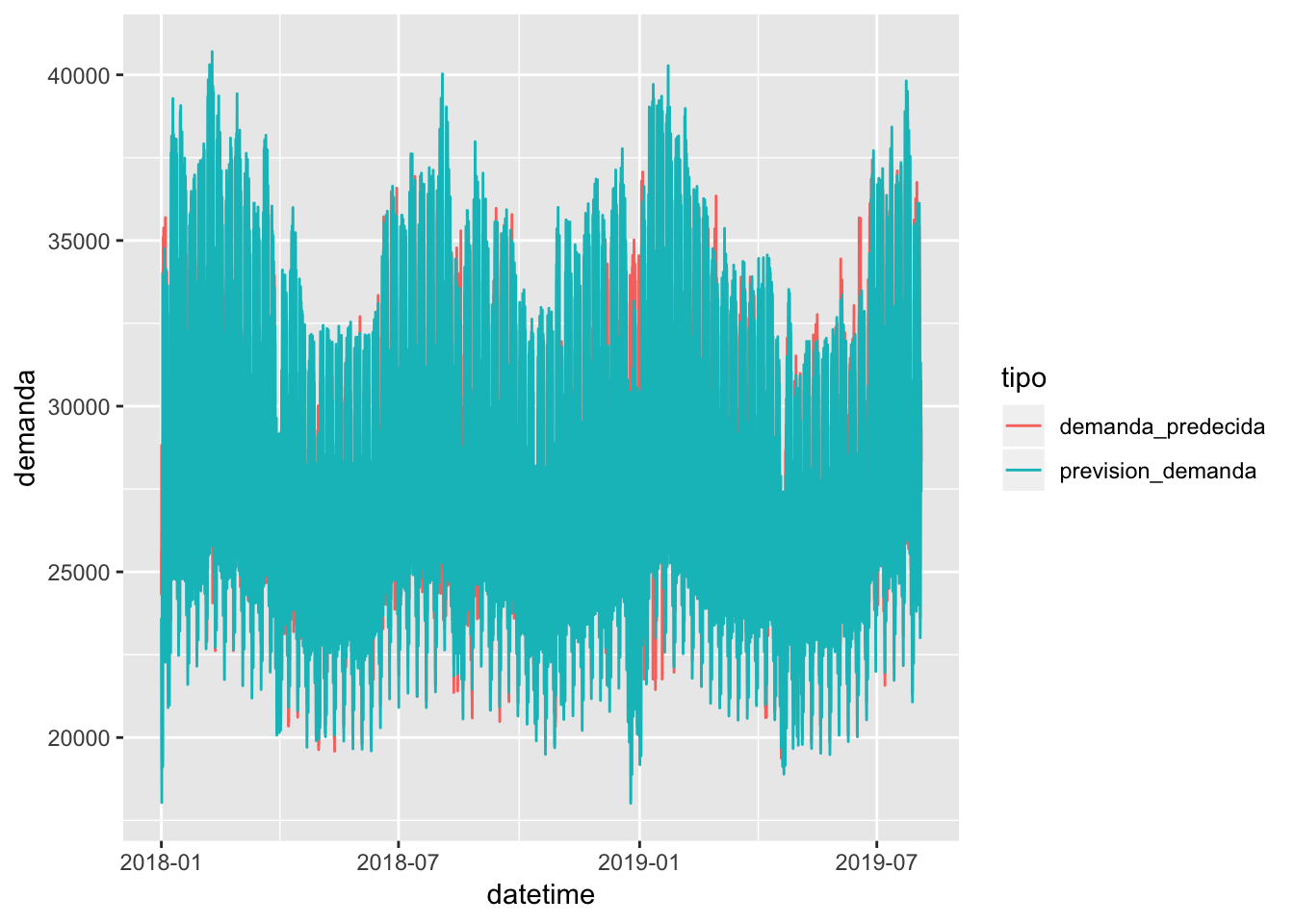
# Gráfico de predicciones vs observaciones en agosto de 2018
testset %>% cbind(demanda_predecida) %>% filter(mes == 8 & year(datetime) <= 2018) %>% select(datetime, prevision_demanda, demanda_predecida) %>% gather(key = tipo, value = demanda, -datetime) %>% ggplot(aes(x = datetime, y = demanda, color = tipo)) + geom_line()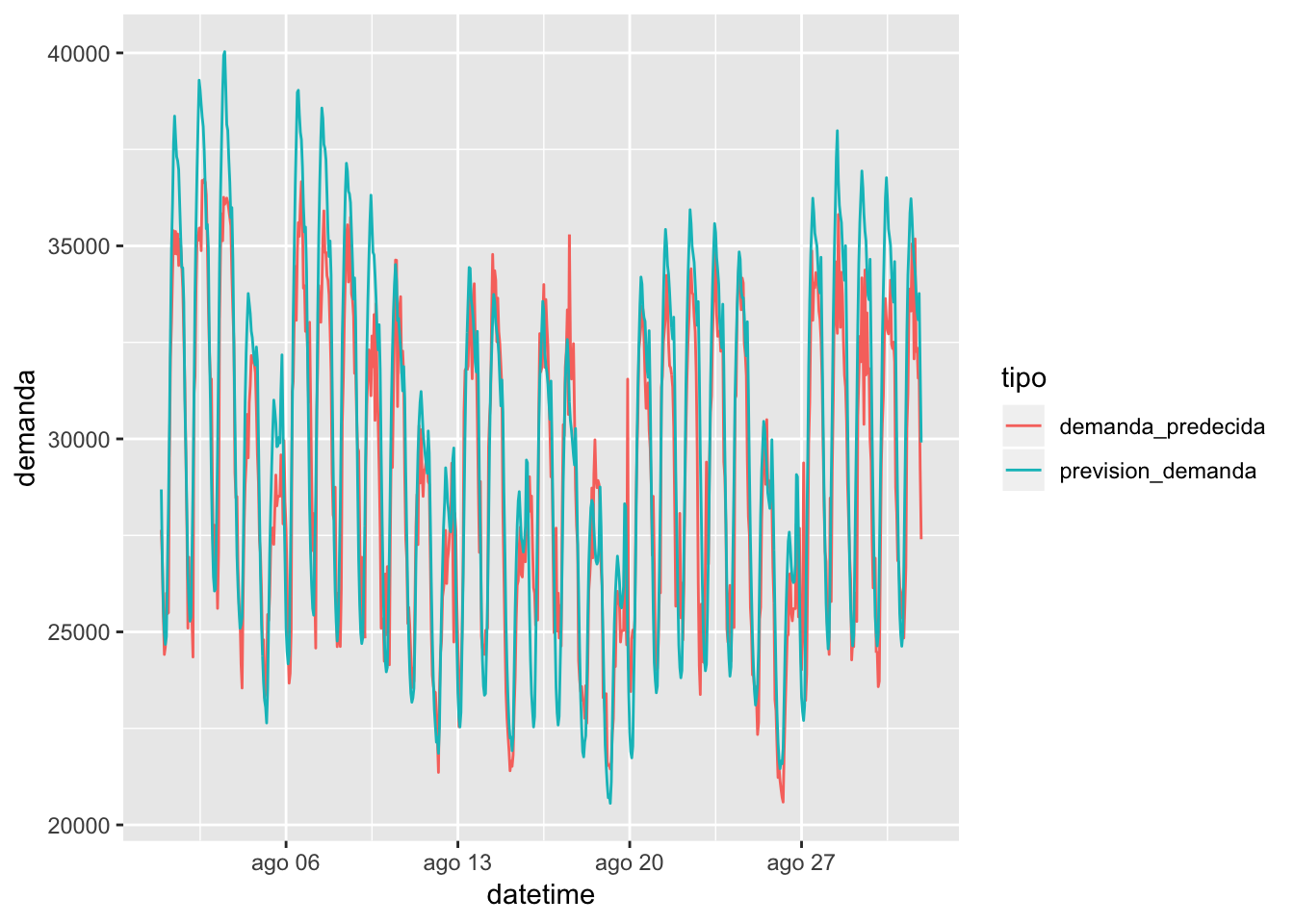
Definitivamente faltan variables que expliquen la variabilidad de los datos, pero con este sencillo modelo se puede intuir cómo se comporta la curva a nivel horario. Si se tuviera una cartera parecida a la del sistema, daría un punto de inicio para comenzar a realizar compras en el mercado diario, aunque obviamente se dispondría del histórico por CUPS, vital para ser más preciso en la altura de la curva.
En la siguiente entrada, demostraré la potencia de trabajar los datos con series temporales y lo compararé con el random forest.