Analizar el impacto de la COVID-19 en la demanda eléctrica parte de la base de que sabemos con qué vamos a comparar dicho impacto, dicho de otro modo: que existe un escenario base de referencia de demanda apto para ser comparado.
Sin embargo, en la mayoría de los casos, los deltas que uno lee en prensa son generalmente siempre referidos a años anteriores. No se pretende que no sea así, pero dichas comparaciones no son todo lo ortodoxas que cabría, al estar comparando circunstancias diferentes de laboralidad y temperatura, y la propia tendencia de desacoplamiento entre PIB y demanda que llevamos años observando. En este ejercicio, lo que pretendo es formular un escenario base de referencia sobre el que poder comparar la demanda real peninsular de 2020 y ver si de este modo se acerca a lo visto en el post anterior. Vamos a ello:
Demanda en b.c. histórica por Comunidad Autónoma
En primer lugar, para ponderar la temperatura por la demanda, necesitaré datos desagregados geográficamente de demanda. Lo más parecido son los balances de energía por Comunidad Autónoma que publica REE en su página de series estadísticas. Aquí hay fundamentalmente dos opciones: descargarse manualmente los datos (de hasta máximo 24 meses con cada consulta) región por región, o hacer uso de su API, bastante más sencilla que la de la página ESIOS. La API resulta cómoda, pero el output en JSON es horrible para tratar, y he decidido descargar las 15 regiones peninsulares en .csv en su lugar.
Una vez descargados, hay que tratarlos, ya que parece que no han estructurado los datos en una tabla, sino que parece un crop de la propia visualización de la web:
library(ggplot2)
library(riem)
library(tidyverse)
library(RCurl)
library(data.table)
library(lubridate)
library(timetk)
library(gt)
library(weathermetrics)
library(tsibble)
library(fable)
library(feasts)
library(fasster)
# Lista demanda mensual por CCAA
list_demanda_CCAA <- list.files("/Users/pherreraariza/Documents/energychisquared/post_inputs/12_post/input_demanda_CCAA", pattern = "balance", full.names = TRUE)
# Leo archivo en una única tabla y limpio datos
demanda_CCAA <- rbindlist(lapply(list_demanda_CCAA, function(file) {
demanda_CCAA_file <- read_delim(file, delim = ",", locale = locale( encoding = "latin1"))
CCAA_name <- demanda_CCAA_file[[1,2]]
demanda_CCAA_header <- c("variable", as.character(demanda_CCAA_file[4,2:25]))
demanda_CCAA_table <- demanda_CCAA_file %>% filter(`Título` == "Demanda en b.c.") %>% mutate_all( ~ str_replace(., ",", "."))
colnames(demanda_CCAA_table) <- demanda_CCAA_header
demanda_CCAA_table <- demanda_CCAA_table %>% mutate(across(!variable, as.numeric),
CCAA = CCAA_name) %>%
filter(variable == "Demanda en b.c.")
demanda_CCAA_table
}))
glimpse(demanda_CCAA)## Rows: 15
## Columns: 26
## $ variable <chr> "Demanda en b.c.", "Demanda en b.c.", "Demanda en b.c.", "De…
## $ `ene/18` <dbl> 950230.9, 454690.9, 1844479.5, 153187.5, 813698.1, 450314.0,…
## $ `feb/18` <dbl> 883557.7, 406832.6, 1717220.7, 143908.8, 741390.3, 429018.6,…
## $ `mar/18` <dbl> 953924.6, 427714.4, 1873335.3, 148671.1, 780145.3, 447419.7,…
## $ `abr/18` <dbl> 878451.3, 395382.1, 1695932.4, 134488.1, 736925.2, 403494.7,…
## $ `may/18` <dbl> 870108.9, 371670.8, 1645679.0, 136589.1, 761407.2, 429690.4,…
## $ `jun/18` <dbl> 836118.9, 386425.1, 1596787.9, 135197.2, 789298.3, 420678.8,…
## $ `jul/18` <dbl> 865999.6, 398805.8, 1607005.1, 147700.9, 902760.7, 409460.9,…
## $ `ago/18` <dbl> 855891.1, 517022.4, 1617145.5, 139379.1, 903149.0, 405988.0,…
## $ `sep/18` <dbl> 847528.7, 454134.4, 1580536.9, 138154.1, 790124.9, 423398.1,…
## $ `oct/18` <dbl> 873135.6, 408719.7, 1637148.8, 147459.7, 729111.6, 439097.8,…
## $ `nov/18` <dbl> 894410.5, 413793.2, 1723854.1, 145925.1, 726074.3, 434543.7,…
## $ `dic/18` <dbl> 920538.9, 436251.1, 1720942.2, 140688.5, 766338.6, 407554.2,…
## $ `ene/19` <dbl> 955695.7, 457953.3, 1831829.7, 157569.4, 841665.4, 463542.5,…
## $ `feb/19` <dbl> 800857.1, 394740.9, 1563729.7, 137243.5, 722984.4, 412888.1,…
## $ `mar/19` <dbl> 819770.8, 388246.9, 1570501.3, 144513.1, 769206.2, 439192.3,…
## $ `abr/19` <dbl> 775652.1, 392573.3, 1498887.1, 133753.6, 717397.6, 409325.0,…
## $ `may/19` <dbl> 775559.0, 371863.6, 1455568.9, 134904.5, 753933.4, 439674.5,…
## $ `jun/19` <dbl> 734051.8, 390596.4, 1403979.9, 133645.4, 781848.1, 431270.9,…
## $ `jul/19` <dbl> 771577.4, 431889.8, 1459713.9, 153082.7, 934973.7, 425913.1,…
## $ `ago/19` <dbl> 751690.8, 482287.4, 1458252.7, 134540.5, 891511.5, 403832.7,…
## $ `sep/19` <dbl> 733274.9, 429438.0, 1437838.6, 136656.0, 740195.6, 424695.6,…
## $ `oct/19` <dbl> 741663.0, 394986.1, 1518709.9, 148674.0, 748991.0, 448901.5,…
## $ `nov/19` <dbl> 762830.4, 414781.0, 1611162.9, 145490.2, 756543.7, 441644.4,…
## $ `dic/19` <dbl> 770472.5, 416962.3, 1639128.2, 141234.6, 777171.5, 408815.5,…
## $ CCAA <chr> "PRINCIPADO DE ASTURIAS", "EXTREMADURA", "GALICIA", "LA RIOJ…Lo importante de estos datos es ver si durante 2018 y 2019 las distribuciones de consumo, o cuotas entre CCAA, permanecen aproximadamente iguales:
cuota_CCAA <- demanda_CCAA %>% pivot_longer(cols = !c(CCAA, variable), names_to = "fecha", values_to = "MWh") %>%
group_by(fecha, CCAA) %>%
summarise(MWh = sum(MWh)) %>%
mutate(freq = MWh / sum(MWh)) %>%
separate(col = fecha, into = c("mes", "año"), sep = "/", remove = FALSE) %>%
mutate(año = as.numeric(año)+2000,
mes = gsub("ene", "01", mes),
mes = gsub("feb", "02", mes),
mes = gsub("mar", "03", mes),
mes = gsub("abr", "04", mes),
mes = gsub("may", "05", mes),
mes = gsub("jun", "06", mes),
mes = gsub("jul", "07", mes),
mes = gsub("ago", "08", mes),
mes = gsub("sep", "09", mes),
mes = gsub("oct", "10", mes),
mes = gsub("nov", "11", mes),
mes = gsub("dic", "12", mes),
fecha = ymd(paste0(año, mes,"01"))) %>%
select(fecha, CCAA, freq)
cuota_CCAA %>% group_by(CCAA) %>% plot_time_series(fecha, freq,
.color_var = year(fecha),
.facet_ncol = 4,
.facet_scales = "free",
.title = "Cuota de demanda en b.c.",
.interactive = FALSE,
.legend_show = FALSE)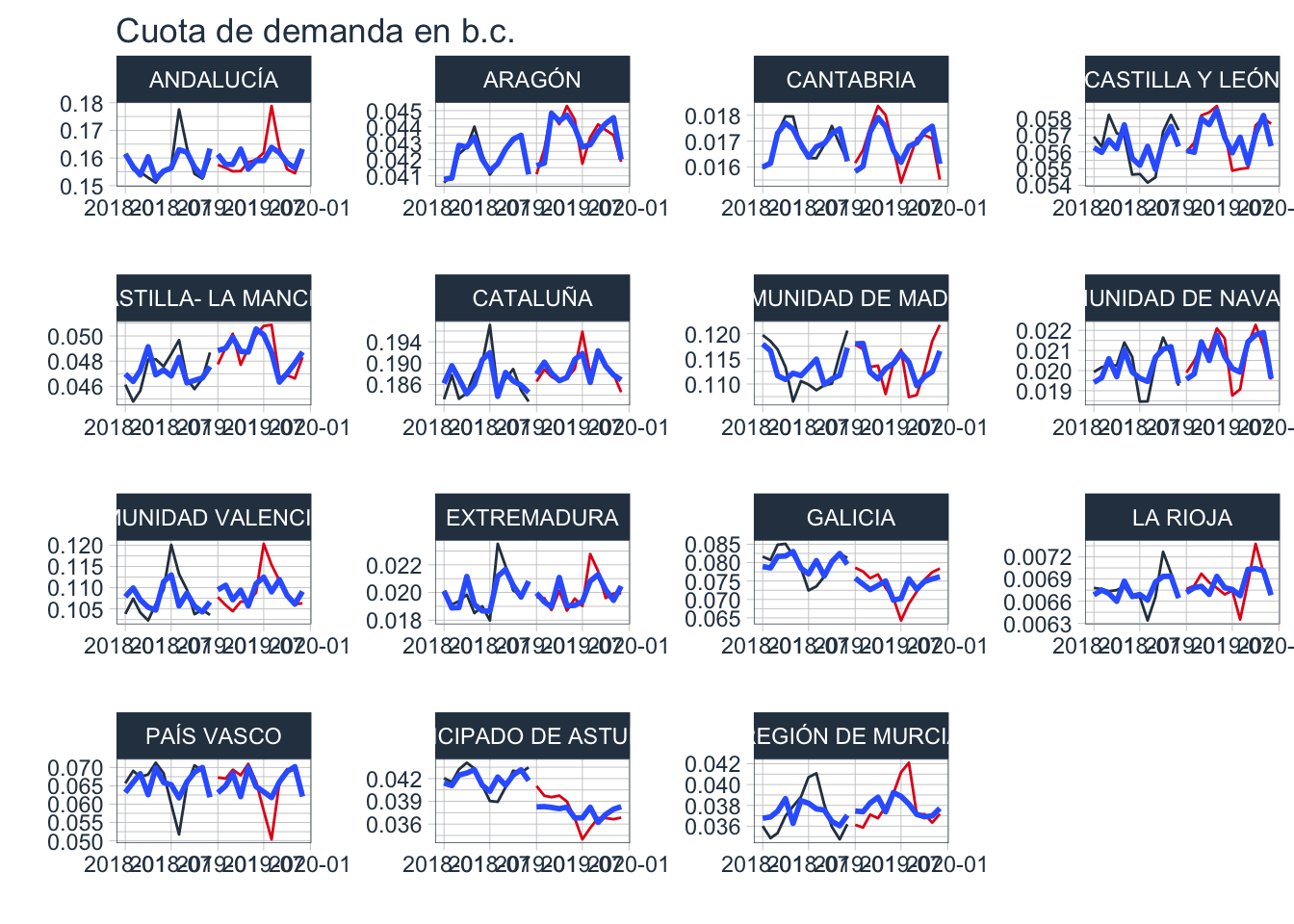
Pese a que hay algunas diferencias, decido utilizar los datos de 2019 para el modelo. Y aquí hago una hipótesis burda, donde supongo que dicho reparto mensual se mantiene igual durante todas las horas del mes. No hay otra forma de disponer los datos horarios de demanda, por lo que no hay más remedio si quiero realizar algún tipo de ponderación de temperaturas. Como las estaciones están repartidas por todo la península, pero dispongo de la ubicación, hago una tabla auxiliar para relacionar dicha ubicación con la tabla de cuotas de demanda por CCAA.
# Trabajo con el año 2019
cuota_CCAA <- cuota_CCAA %>% filter(year(fecha) == 2019) %>% select(CCAA, freq)Datos horarios de temperatura
# Listado de las estaciones de aeropuertos de España
spain_airports <- riem_stations(network = "ES__ASOS")
spain_airports_id <- spain_airports %>% select(id)
spain_airports %>% gt()La lista es bastante extensa, aunque la integridad de los datos es lo crucial. Con la siguiente función, se puede descargar a la ruta que quiera en local los .RData con todos los datos de meteo que haya registrado en ASOS.
Una vez tengo la BBDD de temperaturas, sólo falta leer las estaciones para las cuales nos interesa el estudio (peninsulares) y relacionarlas con cada CCAA para realizar el promedio horario de las estaciones:
# Leo tabla auxilar
CCAA_stations <- read_csv2("/Users/pherreraariza/Documents/energychisquared/post_inputs/12_post/input_demanda_CCAA/CCAA_stations.csv", locale = locale(encoding = "latin1"))
glimpse(CCAA_stations)## Rows: 45
## Columns: 3
## $ id <chr> "LEAB", "LEAL", "LEAM", "LEAS", "LEBZ", "LEBL", "LEBB", "LEBG", …
## $ name <chr> "Albacete", "Alicante", "Almeria", "Aviles", "Badajoz", "Barcelo…
## $ CCAA <chr> "CASTILLA- LA MANCHA", "COMUNIDAD VALENCIANA", "ANDALUCÍA", "PRI…# Leo temperaturas
list_temperaturas <- list.files("/Users/pherreraariza/Documents/Meteo/", pattern = ".rds", full.names = TRUE)
temperaturas <- rbindlist(lapply(list_temperaturas, function(file) {
temperaturas_file <- readRDS(file)
temperaturas_file
}))
# Selecciono y asigno las CCAA de península
temp_peninsular <- temperaturas %>% mutate(tmpf = fahrenheit.to.celsius(tmpf),
datetime = round_date(valid, unit = "hour")) %>%
group_by(station, datetime) %>%
distinct(datetime, .keep_all = TRUE) %>%
select(datetime, station, tmpf) %>%
right_join(CCAA_stations, by = c("station" = "id")) %>%
as_tsibble(index = datetime, key = c(station, CCAA)) %>%
fill_gaps(.full = TRUE) %>%
as.data.frame() %>%
group_by(datetime, CCAA) %>%
summarise(tmpf = mean(tmpf, na.rm =TRUE)) %>%
drop_na(CCAA) %>%
mutate_all(~ifelse(is.nan(.), NA, .))
# Visualizo huecos
temp_peninsular %>% group_by(CCAA, año = year(datetime)) %>% summarise(NAs = sum(is.na(tmpf))) %>% filter(NAs != 0) %>% gt()| año | NAs |
|---|---|
| ANDALUCÍA | |
| 2014 | 12 |
| 2015 | 4 |
| 2016 | 2 |
| 2017 | 1 |
| 2018 | 3 |
| 2019 | 3 |
| 2020 | 3 |
| 2021 | 104 |
| ARAGÓN | |
| 2014 | 22 |
| 2015 | 12 |
| 2016 | 18 |
| 2017 | 2 |
| 2018 | 10 |
| 2019 | 7 |
| 2020 | 8 |
| 2021 | 104 |
| CANTABRIA | |
| 2014 | 2148 |
| 2015 | 2122 |
| 2016 | 1009 |
| 2017 | 7 |
| 2018 | 19 |
| 2019 | 16 |
| 2020 | 14 |
| 2021 | 104 |
| CASTILLA Y LEÓN | |
| 2014 | 2903 |
| 2015 | 2624 |
| 2016 | 2863 |
| 2017 | 2895 |
| 2018 | 2875 |
| 2019 | 2372 |
| 2020 | 34 |
| 2021 | 104 |
| CASTILLA- LA MANCHA | |
| 2014 | 8363 |
| 2015 | 8376 |
| 2016 | 8353 |
| 2017 | 8413 |
| 2018 | 8363 |
| 2019 | 4751 |
| 2020 | 4320 |
| 2021 | 188 |
| CATALUÑA | |
| 2014 | 18 |
| 2015 | 6 |
| 2016 | 4 |
| 2017 | 1 |
| 2018 | 9 |
| 2019 | 5 |
| 2020 | 6 |
| 2021 | 104 |
| COMUNIDAD DE MADRID | |
| 2014 | 16 |
| 2015 | 5 |
| 2016 | 4 |
| 2017 | 2 |
| 2018 | 7 |
| 2019 | 6 |
| 2020 | 7 |
| 2021 | 104 |
| COMUNIDAD DE NAVARRA | |
| 2014 | 1828 |
| 2015 | 1628 |
| 2016 | 1038 |
| 2017 | 15 |
| 2018 | 42 |
| 2019 | 22 |
| 2020 | 23 |
| 2021 | 108 |
| COMUNIDAD VALENCIANA | |
| 2014 | 18 |
| 2015 | 9 |
| 2016 | 4 |
| 2017 | 2 |
| 2018 | 9 |
| 2019 | 6 |
| 2020 | 7 |
| 2021 | 104 |
| EXTREMADURA | |
| 2014 | 8448 |
| 2015 | 8501 |
| 2016 | 8520 |
| 2017 | 8599 |
| 2018 | 8390 |
| 2019 | 8385 |
| 2020 | 8525 |
| 2021 | 267 |
| GALICIA | |
| 2014 | 16 |
| 2015 | 6 |
| 2016 | 4 |
| 2018 | 8 |
| 2019 | 4 |
| 2020 | 6 |
| 2021 | 104 |
| LA RIOJA | |
| 2014 | 8726 |
| 2015 | 8696 |
| 2016 | 8730 |
| 2017 | 8706 |
| 2018 | 8699 |
| 2019 | 8721 |
| 2020 | 8732 |
| 2021 | 272 |
| PAÍS VASCO | |
| 2014 | 19 |
| 2015 | 11 |
| 2016 | 4 |
| 2017 | 1 |
| 2018 | 8 |
| 2019 | 4 |
| 2020 | 6 |
| 2021 | 104 |
| PRINCIPADO DE ASTURIAS | |
| 2014 | 1837 |
| 2015 | 1465 |
| 2016 | 828 |
| 2017 | 36 |
| 2018 | 24 |
| 2019 | 13 |
| 2020 | 17 |
| 2021 | 104 |
| REGIÓN DE MURCIA | |
| 2014 | 2786 |
| 2015 | 2551 |
| 2016 | 2793 |
| 2017 | 2824 |
| 2018 | 1335 |
| 2019 | 35 |
| 2020 | 10 |
| 2021 | 105 |
La datos muestran muchos huecos, para algunas CCAA de casi la totalidad del año. Para corregirlo, se pueden agrupar aquellas CCAA con más huecos y hacer una media horaria con la esperanza de que completen entre todas dichos huecos. Sin embargo, dado que en los años más antiguos casi no se disponen de datos, es más que probable que no se vayan a completar, por lo que introducir en este grupo una CCAA con la mayoría de los datos sea la única solución. Por ello, introduciré Andalucía junto al resto de CCAA sin apenas datos:
# Listado CCAA agrupadas
CCAA_incompletas <- c("CANTABRIA", "CASTILLA Y LEÓN", "CASTILLA- LA MANCHA", "COMUNIDAD DE NAVARRA", "EXTREMADURA", "LA RIOJA", "PRINCIPADO DE ASTURIAS", "REGIÓN DE MURCIA", "ANDALUCÍA")
# Creo grupo_1 con las CCAA agrupadas
temp_peninsular_corregido <- temp_peninsular %>% mutate(CCAA_agrupadas = case_when(
CCAA %in% CCAA_incompletas ~ "grupo_1",
TRUE ~ CCAA))
# Detecto huecos a nivel anual
temp_peninsular_anual <- temp_peninsular_corregido %>% group_by(datetime, CCAA_agrupadas) %>%
summarise(tmpf = mean(tmpf, na.rm =TRUE)) %>%
drop_na(CCAA_agrupadas) %>%
mutate_all(~ifelse(is.nan(.), NA, .)) %>%
group_by(CCAA_agrupadas, año = year(datetime)) %>%
summarise(NAs = sum(is.na(tmpf))) %>%
filter(NAs != 0)
# Visualizo huecos
gt(temp_peninsular_anual)| año | NAs |
|---|---|
| ARAGÓN | |
| 2014 | 22 |
| 2015 | 12 |
| 2016 | 18 |
| 2017 | 2 |
| 2018 | 10 |
| 2019 | 7 |
| 2020 | 8 |
| 2021 | 104 |
| CATALUÑA | |
| 2014 | 18 |
| 2015 | 6 |
| 2016 | 4 |
| 2017 | 1 |
| 2018 | 9 |
| 2019 | 5 |
| 2020 | 6 |
| 2021 | 104 |
| COMUNIDAD DE MADRID | |
| 2014 | 16 |
| 2015 | 5 |
| 2016 | 4 |
| 2017 | 2 |
| 2018 | 7 |
| 2019 | 6 |
| 2020 | 7 |
| 2021 | 104 |
| COMUNIDAD VALENCIANA | |
| 2014 | 18 |
| 2015 | 9 |
| 2016 | 4 |
| 2017 | 2 |
| 2018 | 9 |
| 2019 | 6 |
| 2020 | 7 |
| 2021 | 104 |
| GALICIA | |
| 2014 | 16 |
| 2015 | 6 |
| 2016 | 4 |
| 2018 | 8 |
| 2019 | 4 |
| 2020 | 6 |
| 2021 | 104 |
| grupo_1 | |
| 2014 | 12 |
| 2015 | 4 |
| 2016 | 2 |
| 2017 | 1 |
| 2018 | 3 |
| 2019 | 3 |
| 2020 | 2 |
| 2021 | 101 |
| PAÍS VASCO | |
| 2014 | 19 |
| 2015 | 11 |
| 2016 | 4 |
| 2017 | 1 |
| 2018 | 8 |
| 2019 | 4 |
| 2020 | 6 |
| 2021 | 104 |
Ahora el número de huecos es mucho más manejable, y puedo interpolar con algún modelo para rellenar cada una de las series:
# Tabla con temperatura en formato tsibble
temp_peninsular_tsibble <- temp_peninsular_corregido %>%
select(datetime, tmpf, CCAA_agrupadas) %>%
group_by(datetime, CCAA_agrupadas) %>%
summarise(tmpf = mean(tmpf, na.rm = TRUE)) %>%
mutate(tmpf = ifelse(is.nan(tmpf), NA, tmpf)) %>%
tsibble(key = CCAA_agrupadas, index = datetime)
# Interpolación de huecos
temp_peninsular_interpolado <- temp_peninsular_tsibble %>%
model(naive = ARIMA(tmpf ~ -1 + pdq(0,1,0) + PDQ(0,0,0))) %>%
interpolate(temp_peninsular_tsibble)
# Visualización de temperaturas
temp_peninsular_interpolado %>% plot_time_series(.date_var = datetime, .value = tmpf, .facet_vars = CCAA_agrupadas, .facet_ncol = 2, .interactive = FALSE)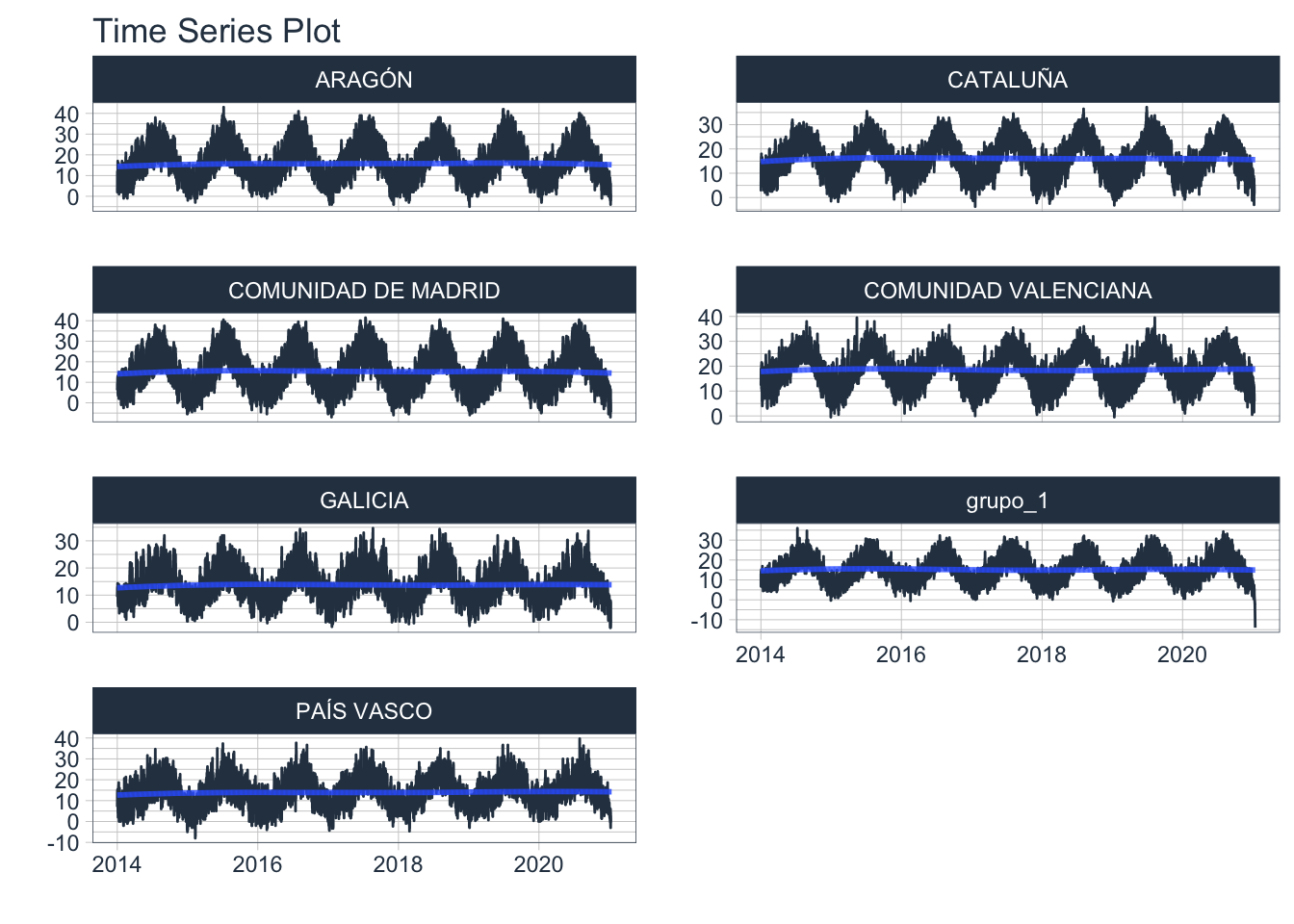 Ahora, con las series completas, puedo ponderarlo con las cuotas de las CCAA agrupadas que tengo, y de esta manera tener una aproximación a la temperatura media histórica peninsular:
Ahora, con las series completas, puedo ponderarlo con las cuotas de las CCAA agrupadas que tengo, y de esta manera tener una aproximación a la temperatura media histórica peninsular:
# Agrupación frecuencias para grupo_1
cuota_CCAA_agrupadas <- cuota_CCAA %>% mutate(CCAA_agrupadas = case_when(
CCAA %in% CCAA_incompletas ~ "grupo_1",
TRUE ~ CCAA)) %>%
group_by(CCAA_agrupadas) %>%
summarise(freq = sum(freq))
# Obtención tabla temperatura peninsular
temp_peninsular_ponderado <- temp_peninsular_interpolado %>% left_join(cuota_CCAA_agrupadas, by = "CCAA_agrupadas") %>%
index_by(datetime) %>%
summarise(tmp_ponderada = weighted.mean(tmpf, freq)) %>%
index_by(fecha = date(datetime)) %>%
summarise(tmp_ponderada = max(tmp_ponderada))
# Visualización temperatura
temp_peninsular_ponderado %>% plot_time_series(.date_var = fecha, .value = tmp_ponderada, .interactive = FALSE)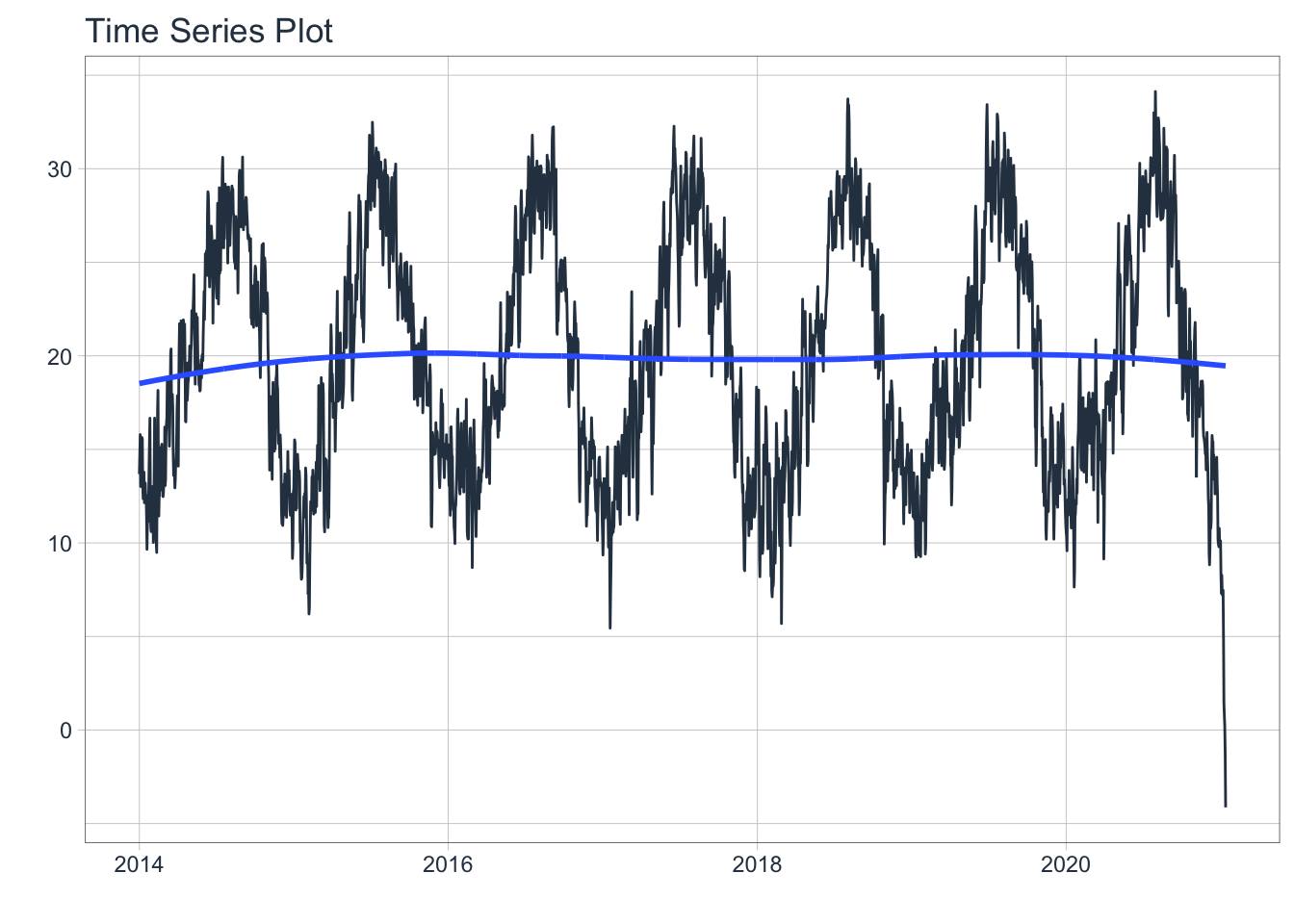 Hay un pico de temperaturas mínimas en 2021 (que afortunadamente no utilizaré), pero que manifiestan el problema de las medias de las regiones con menos datos: son al mismo tiempo regiones con climatología continental y con mínimos de temperatura que arrastran la distribución de los valores. Se podría corregir asignando un peso por población, por ejemplo, pero no he querido llegar mucho más lejos para el ejemplo.
Hay un pico de temperaturas mínimas en 2021 (que afortunadamente no utilizaré), pero que manifiestan el problema de las medias de las regiones con menos datos: son al mismo tiempo regiones con climatología continental y con mínimos de temperatura que arrastran la distribución de los valores. Se podría corregir asignando un peso por población, por ejemplo, pero no he querido llegar mucho más lejos para el ejemplo.
Modelo
Para la tabla de input de datos final a escala diaria, ya solo falta la demanda (descargable desde la página de ESIOS) y una lista de fechas con los festivos nacionales para crear una variable dummy que discrmine entre laborables y festivos (incluyendo fines de semana):
# Lectura demanda
demanda_real <- read_csv2("/Users/pherreraariza/Documents/energychisquared/post_inputs/11_post/demanda_real/demanda_real.csv") %>% select(datetime, value) %>% rename(MWh = value)
# Lectura festivos
festivos <- read_csv2("/Users/pherreraariza/Documents/energychisquared/post_inputs/11_post/festivos.csv", col_types = "cc") %>% mutate(fecha = dmy(fecha))
# Join con tabla final para modelizar
demanda <- demanda_real %>% group_by(fecha = date(datetime)) %>%
summarise(MWh = sum(MWh, na.rm = TRUE)) %>%
mutate(weekday = wday(fecha, label = TRUE)) %>%
left_join(festivos, by = "fecha") %>%
mutate(tipo = factor(if_else(is.na(tipo) & weekday %in% c("lun","mar", "mié", "jue", "vie"), "L", "F"))) %>%
left_join(temp_peninsular_ponderado, by = "fecha") %>%
select(fecha, tipo, MWh, tmp_ponderada)
# Visualización
glimpse(demanda) ## Rows: 2,557
## Columns: 4
## $ fecha <date> 2014-01-01, 2014-01-02, 2014-01-03, 2014-01-04, 2014-0…
## $ tipo <fct> F, L, L, F, F, F, L, L, L, L, F, F, L, L, L, L, L, F, F…
## $ MWh <dbl> 552505.8, 676598.3, 683164.3, 644651.8, 608006.3, 57373…
## $ tmp_ponderada <dbl> 13.679719, 14.722614, 15.789024, 13.014828, 13.590476, …Para el modelo, el enfoque radica en tratar el dataset como una serie temporal, y trabajar con los términos que permita cada uno de los tres métodos que emplearé:
- Término temperatura diaria: como variable exógena, cuya representación vs la demanda indica una relación cuadrática (Hyndman et al.), con un punto de inflexíón en torno a los 20 ºC.
- Término para el tipo de día: booleano que indica si se trata de fin de semana o festivo vs laborable.
- Término para la estacionalidad semanal: aplciable a través de un término de Fourier.
- Término para la estacionalidad anual: aplciable a través de un término de Fourier.
# Relación cuadrátiva Temperatura vs Demanda
demanda %>% ggplot(aes(x = tmp_ponderada, y = MWh, col = tipo)) +
geom_point(alpha = 0.6) +
labs(x="Temperatura (ºC)", y = "Demanda (MWh)")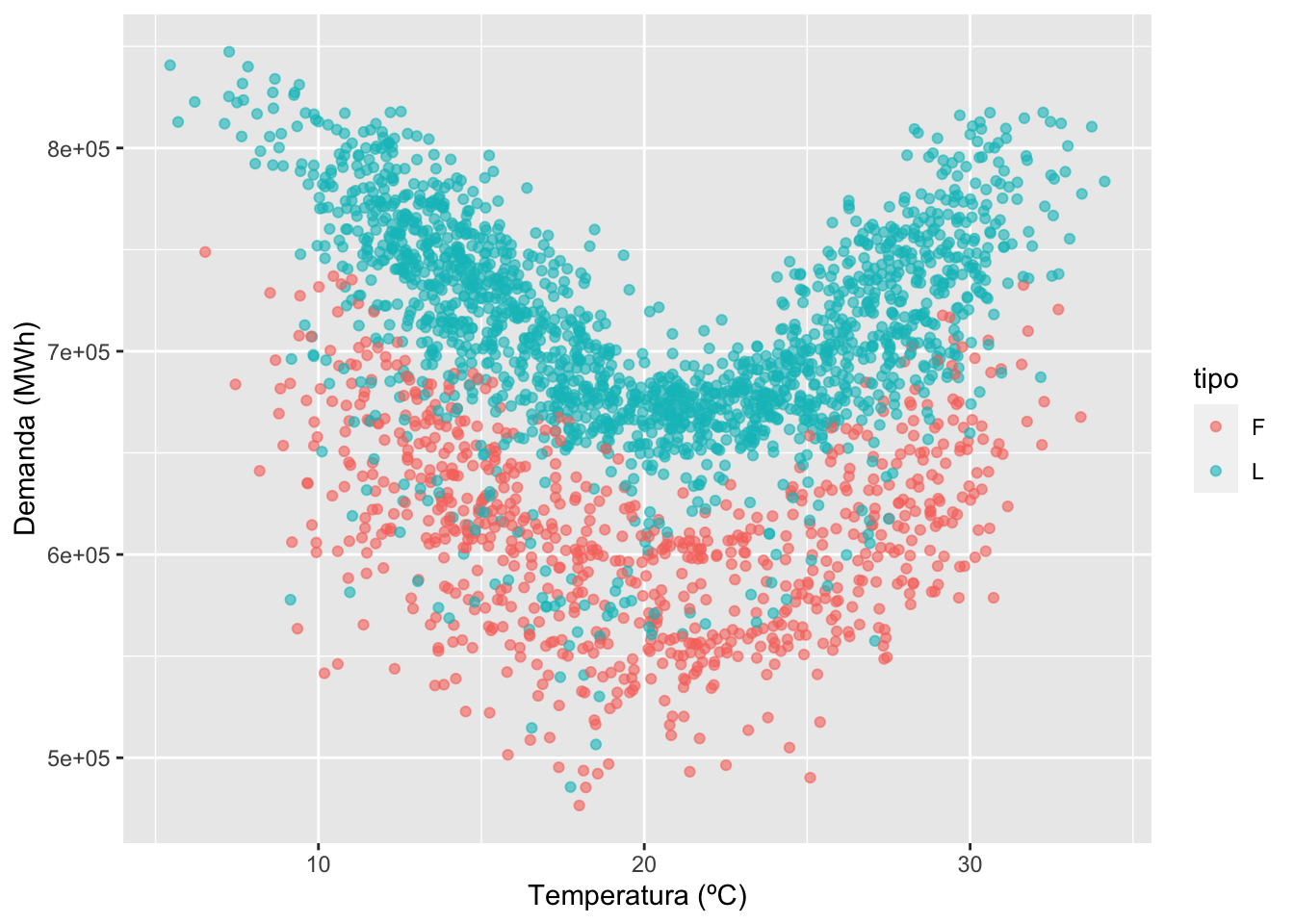 Se crean tres sets de datos: el de entrenamiento (5 años de datos), el de test (año 2019), que permitirá evaluar los errores y la bondad del modelo, y finalmente el de validación que será el año de estudio, 2020.
Se crean tres sets de datos: el de entrenamiento (5 años de datos), el de test (año 2019), que permitirá evaluar los errores y la bondad del modelo, y finalmente el de validación que será el año de estudio, 2020.
Para el set de entrenamiento pruebo con un método ARIMA, corrigiendo la varianza a través del logaritmo del outcome, incorporando la relación cuadrática de la temperatura, los términos de Fourier para la estacionalidad y el booleano con el tipo de día. Asímismo, fuerzo los términos PDQ a (0,0,0) para tratar de emular ruido blanco.
También pruebo con una regresión lineal (TSLM) y un método de redes neuronales (computacionalmente más costoso para el set de datos, aviso), y finalmente una combinación de los tres haciendo una media para cada valor:
# Set de entrenamiento
train_set <- demanda %>% filter(year(fecha) <= 2018) %>%
as_tsibble(index = fecha)
# Set de test
test_set <- demanda %>% filter(year(fecha) == 2019) %>%
as_tsibble(index = fecha)
# Set de validación
validation_set <- demanda %>% filter(year(fecha) == 2020) %>%
as_tsibble(index = fecha)
# Modelo
fit <- train_set %>% model(ARIMA = ARIMA(log(MWh) ~ PDQ(0, 0, 0) + pdq(d=0) + tmp_ponderada + I(tmp_ponderada^2) + tipo + fourier(period = "week", K = 3) + fourier(period = "year", K = 3)),
TSLM = TSLM(log(MWh) ~ tmp_ponderada + I(tmp_ponderada^2) + tipo + fourier(period = "week", K = 3) + fourier(period = "year", K = 3)),
NNETAR = NNETAR(box_cox(MWh, 0.15) ~ AR() + tmp_ponderada + I(tmp_ponderada^2))) %>%
mutate(COMBINATION = (ARIMA + TSLM + NNETAR) / 3)
# KPI modelo
fit %>% accuracy()## # A tibble: 4 x 9
## .model .type ME RMSE MAE MPE MAPE MASE ACF1
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 ARIMA Training 282. 14370. 9569. -0.0126 1.43 0.323 0.0140
## 2 TSLM Training 503. 26185. 19489. -0.0756 2.87 0.657 0.719
## 3 NNETAR Training 183. 11132. 6800. -0.0186 1.02 0.229 -0.0158
## 4 COMBINATION Training 354. 13318. 9358. -0.0311 1.39 0.316 0.454fit %>% select(COMBINATION) %>% gg_tsresiduals()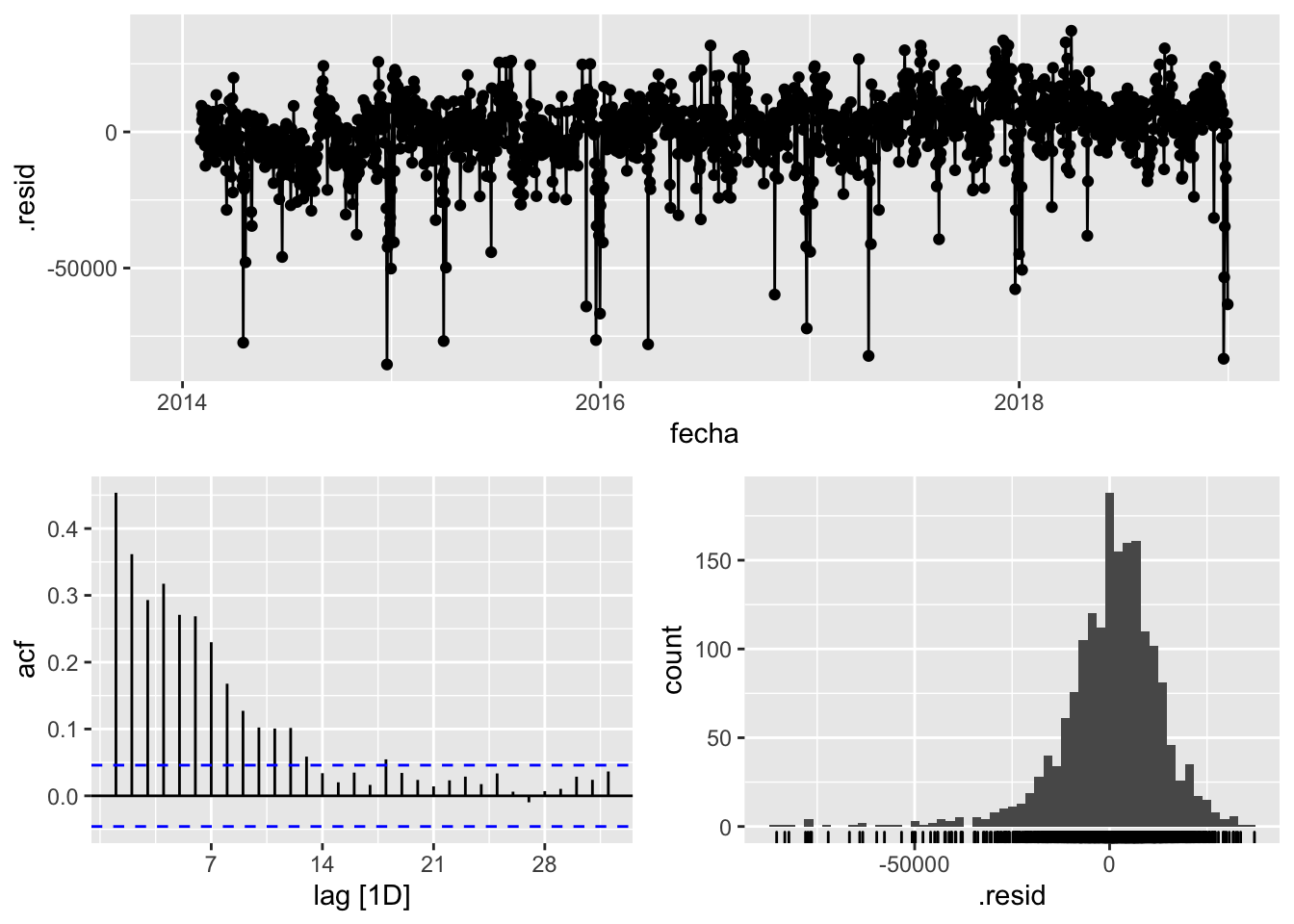
Los resultados son prometedores para la red neuronal, aunque la distribución de los errores parece indicar que aún queda mucha información en el remanente por ser explicada. Por otra parte, para tomar qué modelo utilizar para el añom 2020, hay que comprobar si sufre de over-fitting o no, y esto se podrá ver con el set de datos de test para el año 2019:
# Forecast test set
forecast_test <- fit %>% forecast(test_set, times = 10)
# KPI sobre test
forecast_test %>% accuracy(test_set)## # A tibble: 4 x 9
## .model .type ME RMSE MAE MPE MAPE MASE ACF1
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 ARIMA Test 3090. 31710. 22426. 0.225 3.27 NaN 0.858
## 2 COMBINATION Test 2908. 28085. 20470. 0.175 3.04 NaN 0.604
## 3 NNETAR Test 5332. 52541. 41572. 0.391 6.23 NaN 0.417
## 4 TSLM Test -22.5 26954. 18499. -0.138 2.73 NaN 0.688forecast_test %>% autoplot(test_set, level = NULL) + labs(y = "Demanda (MWh) 2019")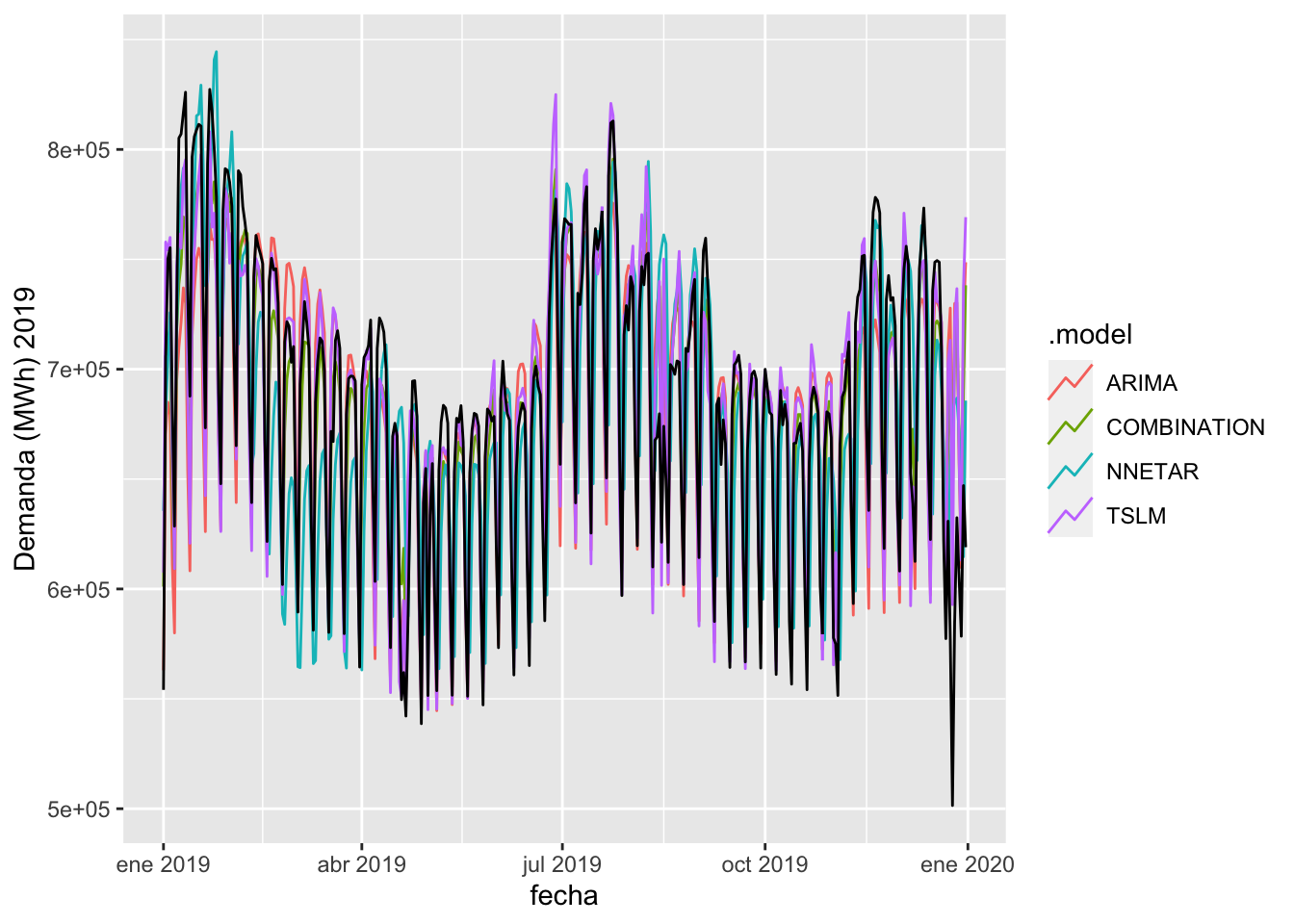 Efectivamente la red neuronal padecía de un sobreajuste sobre el set de entrenamiento, al multiplicar su error por más de 8 en el set de test. El modelo que mejor se comporta es la regresión lineal con variables exógenas (TSLM), que será por tanto el que utilice para el análisis del año 2020.
Efectivamente la red neuronal padecía de un sobreajuste sobre el set de entrenamiento, al multiplicar su error por más de 8 en el set de test. El modelo que mejor se comporta es la regresión lineal con variables exógenas (TSLM), que será por tanto el que utilice para el análisis del año 2020.
# Forecast final sobre 2020
forecast_test_2020 <- fit %>% select(TSLM) %>% forecast(validation_set)
# Visualización
forecast_test_2020 %>% autoplot(validation_set, level = NULL) + labs(y = "Demanda (MWh) 2020")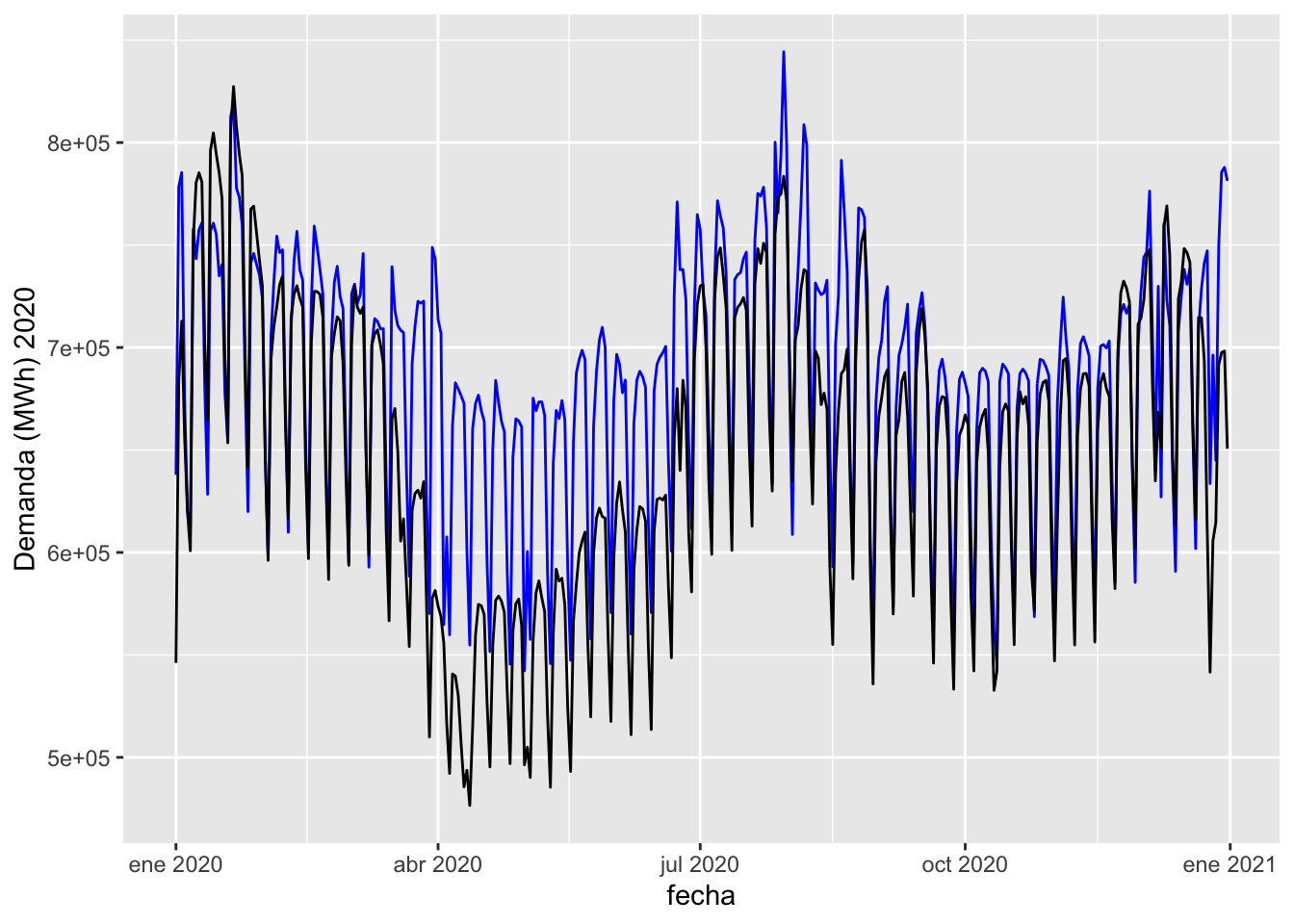
La línea negra indica la demanda real observada y publicada por REE, mientras que la azul corresponde a la simulación de lo que considero sería el escenario base con el que contrastar el efecto de la pandemia. Claramente, se obversva el tremendo impacto a partir de mediados de marzo y cómo existe una cierta recuperación en verano, sin llegar a ser del 100%. Es únicamente en diciembre cuando parece que las líneas se llegan a solapar con mayor claridad, indicando una recuperación que sería indistinguible del propio error del modelo.
De forma análoga a como hice en el post previo de análisis de la demanda de la COVID-19 sobre la demanda eléctrica, se puede graficar el impacto mensual acumulado para ver si aproximadamente coincide o no:
# Impacto 2020 de COVID vs escenario base forecasteado
forecast_test_2020 %>% as_tibble() %>%
select(fecha, .mean) %>%
left_join(validation_set, by = "fecha") %>%
rename(base = .mean,
real = MWh) %>%
group_by(month = yearmonth(fecha)) %>%
summarise(base = sum(base, na.rm = TRUE),
real = sum(real, na.rm = TRUE)) %>%
mutate(year = year(month),
month = month(month, label = TRUE)) %>%
mutate(cum_base = cumsum(base),
cum_real = cumsum(real)) %>%
mutate(delta = ((cum_real/cum_base)-1)*100) %>%
ggplot(aes(x = month, y = delta, group = 1)) + geom_line(color = "blue") +
geom_point(color = "blue") + geom_text(aes(label = round(delta, 1)), vjust = "inward", hjust = "inward", show.legend = FALSE) +
ggtitle("Delta acumulado respecto al forecast base") + ylab("%") + xlab("Mes") 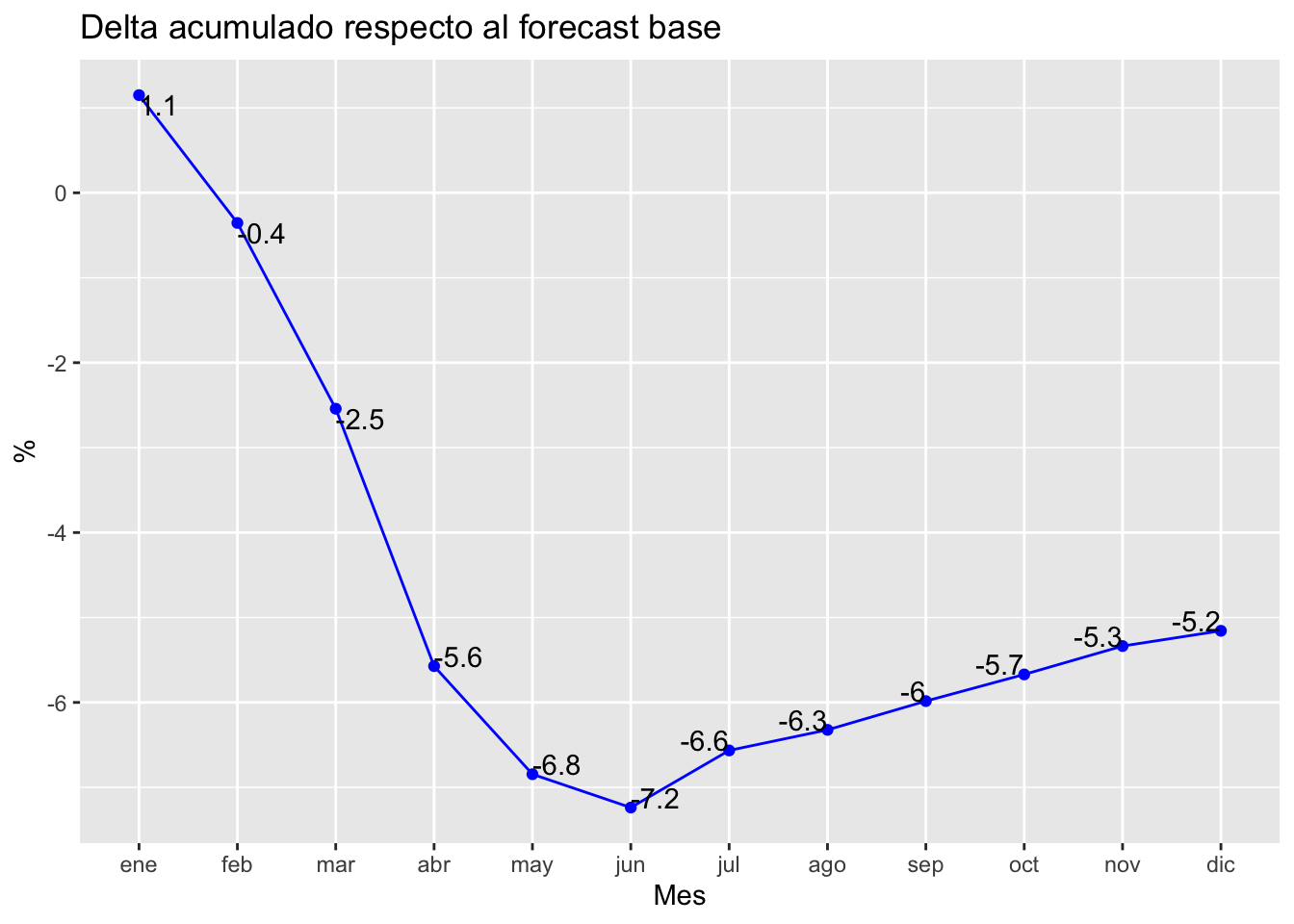
Tal y como se muestra, el impacto total acumulado simulado es del -5.2%, cercano al -5.75% que mostraba en el anterior análisis, donde el escenario base era la media de la demanda desde 2017 a 2019, ambos incluidos. También es cierto que la simulación ya parte que para el mes de enero de 2020 se consumió un 1.1% más de los esperado, por lo que toda la altura de la curva acumulada habría que enrasarla al cero. Aún así, me parece un análisis más limpio que contar o comparar con medias de años anteriores.