En los últimos meses, la generación hidráulica ha dado de qué hablar en el sector eléctrico. Diferentes medios han afirmado (aquí o aquí) que esta tecnología estaba marcando precio marginal en el mercado spot con unos valores más elevados de lo habitual.
En el presente análisis, expongo cómo se hace un EDA o Análisis Exploratorio de Datos para intuir si estas afirmaciones son percepciones estadísticamente relacionables con la realidad. Comenzaré cargando los datos básicos que necesito:
library(readr)
library(dplyr)
library(tidyr)
library(lubridate)
library(ggplot2)
library(forecast)
library(ggstatsplot)
library(broom)
library(knitr)
library(factoextra)
library(kableExtra)
# Leo los datos
generacion_UGH <- read_csv2("/Users/pherreraariza/Documents/ModeloESIOS/UGH.csv", skip = 1, col_names = c("datetime", "variable", "UGH")) %>% select(-variable)
omie <- read_csv2("/Users/pherreraariza/Documents/ModeloESIOS/omie.csv", skip = 1, col_names = c("datetime", "variable", "omie")) %>% select(-variable)
demanda <- read_csv2("/Users/pherreraariza/Documents/ModeloESIOS/demanda.csv", skip = 1, col_names = c("datetime", "variable", "demanda")) %>% select(-variable)
embalses <- read_csv2("/Users/pherreraariza/Documents/ModeloESIOS/embalses/reservas.csv", skip = 0, col_names = TRUE) %>% mutate(fecha = dmy(fecha))
# Generamos la tabla horaria
datos_horarios <- omie %>% left_join(generacion_UGH, by = "datetime") %>%
left_join(demanda, by = "datetime") %>%
mutate(fecha = as.Date(datetime)) %>%
left_join(embalses, by ="fecha") %>%
mutate(UGH_fraction = (UGH / demanda) * 100,
weekday = as.factor(wday(datetime)),
tipo = if_else(weekday %in% c(2,3,4,5,6), "L", "F"),
mes = month(datetime),
quarter = as.factor(ceiling(mes / 3)),
año = as.factor(year(datetime)))Tradicionalmente, la generación hidráulica de embalse (codificada por REE con la abreviatura UGH), ha sido una fuente que deprimía el precio spot, conjuntamente con la eólica, nuclear y solar. Sin embargo, cabe analizar los datos para ver qué ha pasado históricamente y si hay fundamento estadístico para pensar que ahora se vive una situación sustancialmente diferente.
Utilizaré para este análisis exploratorio las siguientes fuentes de información:
- REE, consultando su web pública ESIOS: de donde se disponen los datos horarios de producción hidroeléctrica (UGH), demanda programada y precio OMIE.
- Boletín hidrólogico semanal, del actual Ministerio de Transición Ecoógica, para recoger los datos de energía hidroeléctrica máxima disponible.
El horizonte de datos contempla desde el 1 de enero de 2014 hasta el 14 de agosto de 2018. Existe un problema evidente de asignación entre los datos semanales (pasados a diarios por interpolación), y los datos de REE, de naturaleza horaria. Asumo que horariamente, el nivel de los embalses se mantiene constante, o más bien, asumo que no tendrá demasiado efecto sobre el análisis.
Nivel de los embalses
En primer lugar, cabe contextualizar la producción UGH al nivel de producible, esto es, al nivel máximo teórico producible. Para ello, se puede graficar la evolución de dicho nivel a lo largo de los años:
# Convertimos embalses a ts
embalses_ts <- embalses %>% select(reservas) %>% ts(start = c(2014, 1), end = c(2018, 226), frequency = 365)
# Gráfico evolutivo y seasonal
embalses_ts %>% autoplot() +
ggtitle("Evolución del nivel energía embalsada") +
xlab("Fecha") +
ylab("GWh")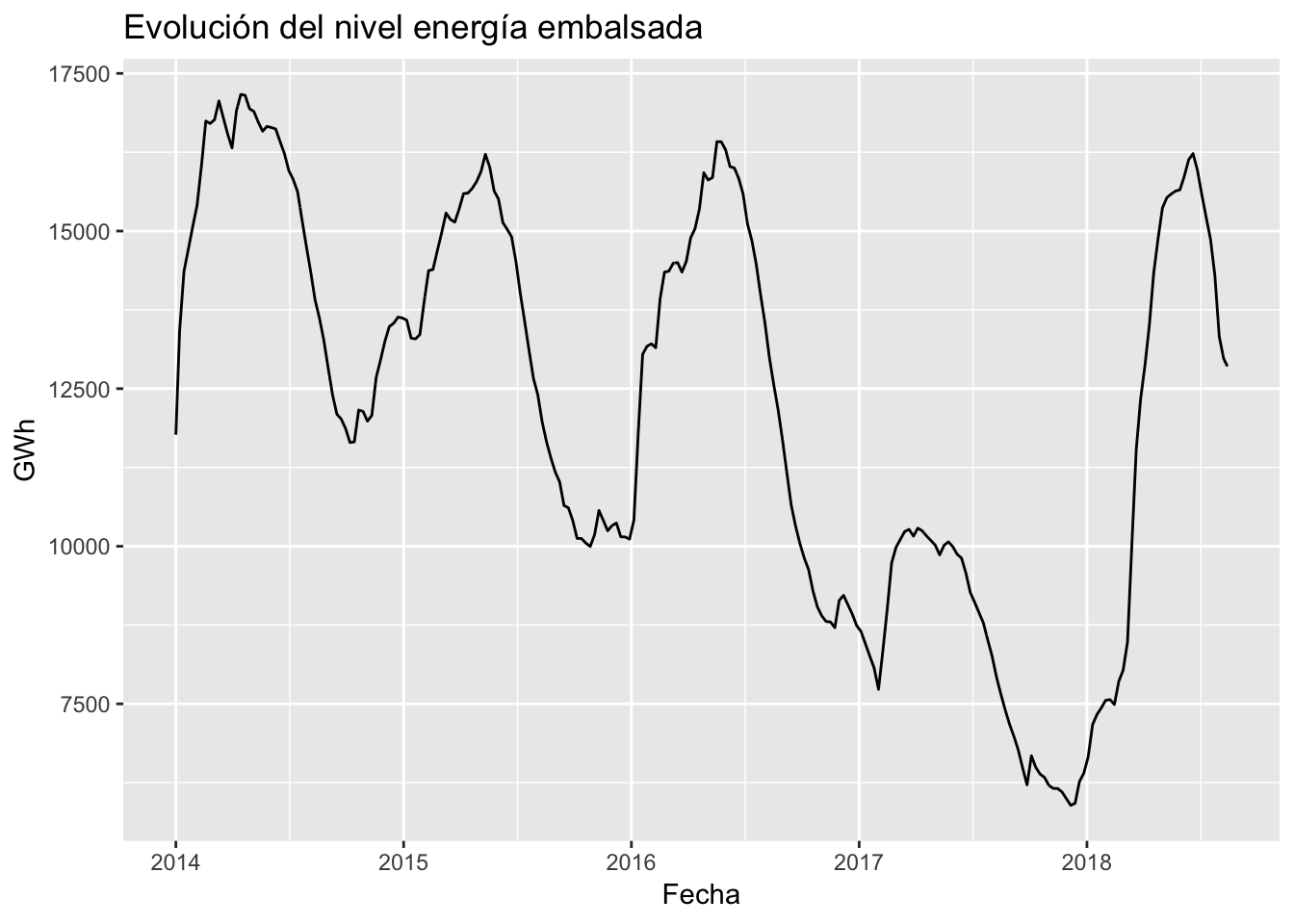
embalses_ts %>% ggseasonplot(year.labels=TRUE, year.labels.left=TRUE, polar=FALSE) +
ggtitle("Evolución estacional nivel energía embalsada") +
xlab("Fecha") +
ylab("GWh")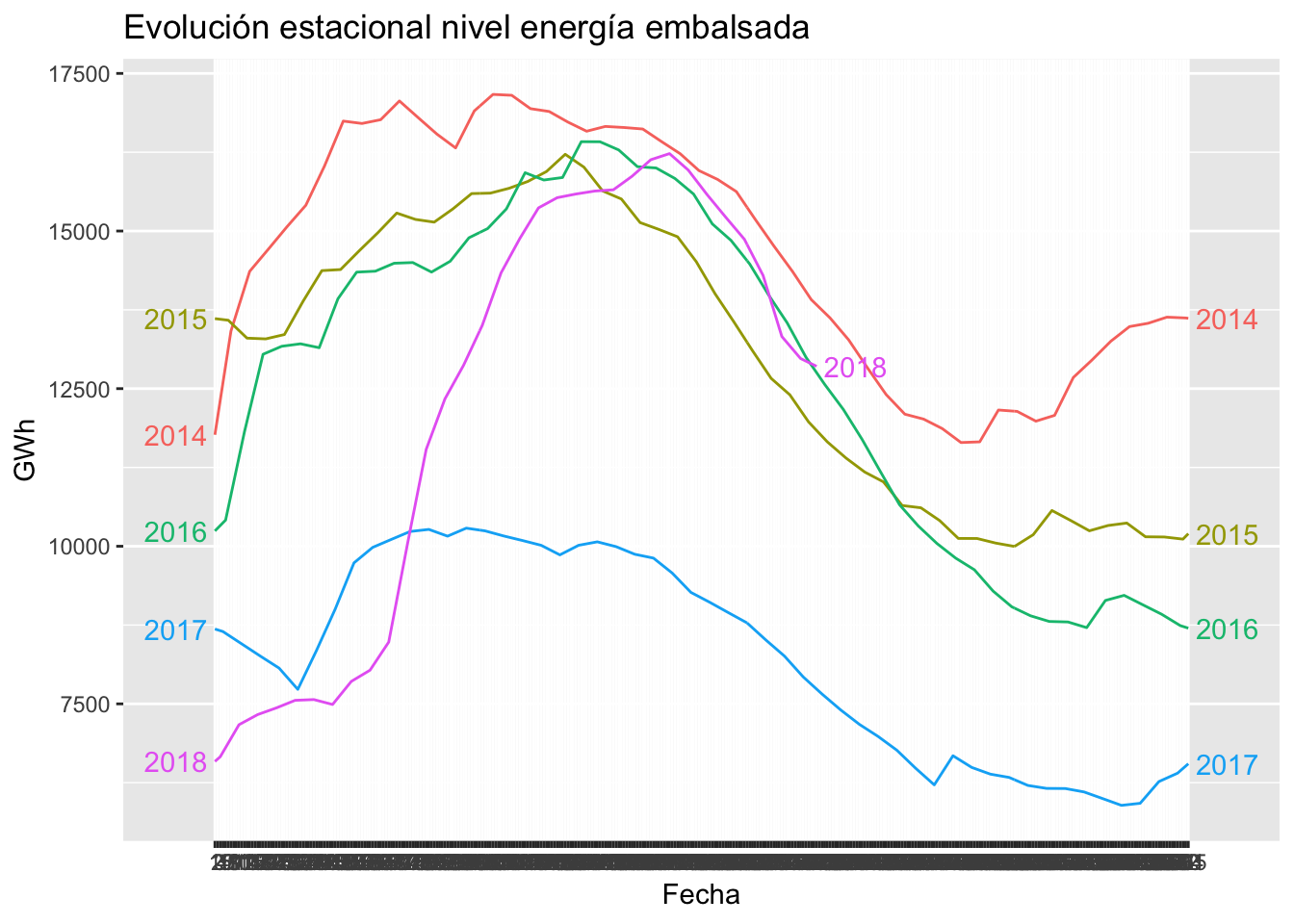
El año 2017 fue excepcionalmente seco, con las reservas a aproximadamente la mitad del histórico de los últimos años, y sin embargo, entre el Q1 y el Q2 de 2018 se recuperaron hasta los niveles habituales. Anteriomente, el año 2014 parece ser un año muy húmedo, donde destaca especialmente el Q4 al aumentar significativamente las reservas de energía hidroeléctrica.
Distribución de la energía hidroeléctrica generada
En cualquier análisis exploratorio de datos (EDA), es conveniente abordar la distribución de los datos. Como se dispone de una granularidad horaria, se pueden agregar los datos como se quiera. A mí, particularmente me gusta verlo por quarters, ya que aparte del producto anual, en general, las comercializadoras tienden a realizar sus coberturas por quarters en cuanto comienzan a disponer de liquidez.
La distribución de dicha generación ha sido como sigue:
datos_horarios %>% filter(tipo == "L") %>%
ggplot(aes(x = UGH)) +
geom_density(aes(x = UGH, fill = quarter, color = quarter, alpha = 0.10)) +
facet_grid(. ~ año) +
ggtitle("Producción hidroeléctrica UGH por quarter") + xlab("MWh") + ylab("densidad")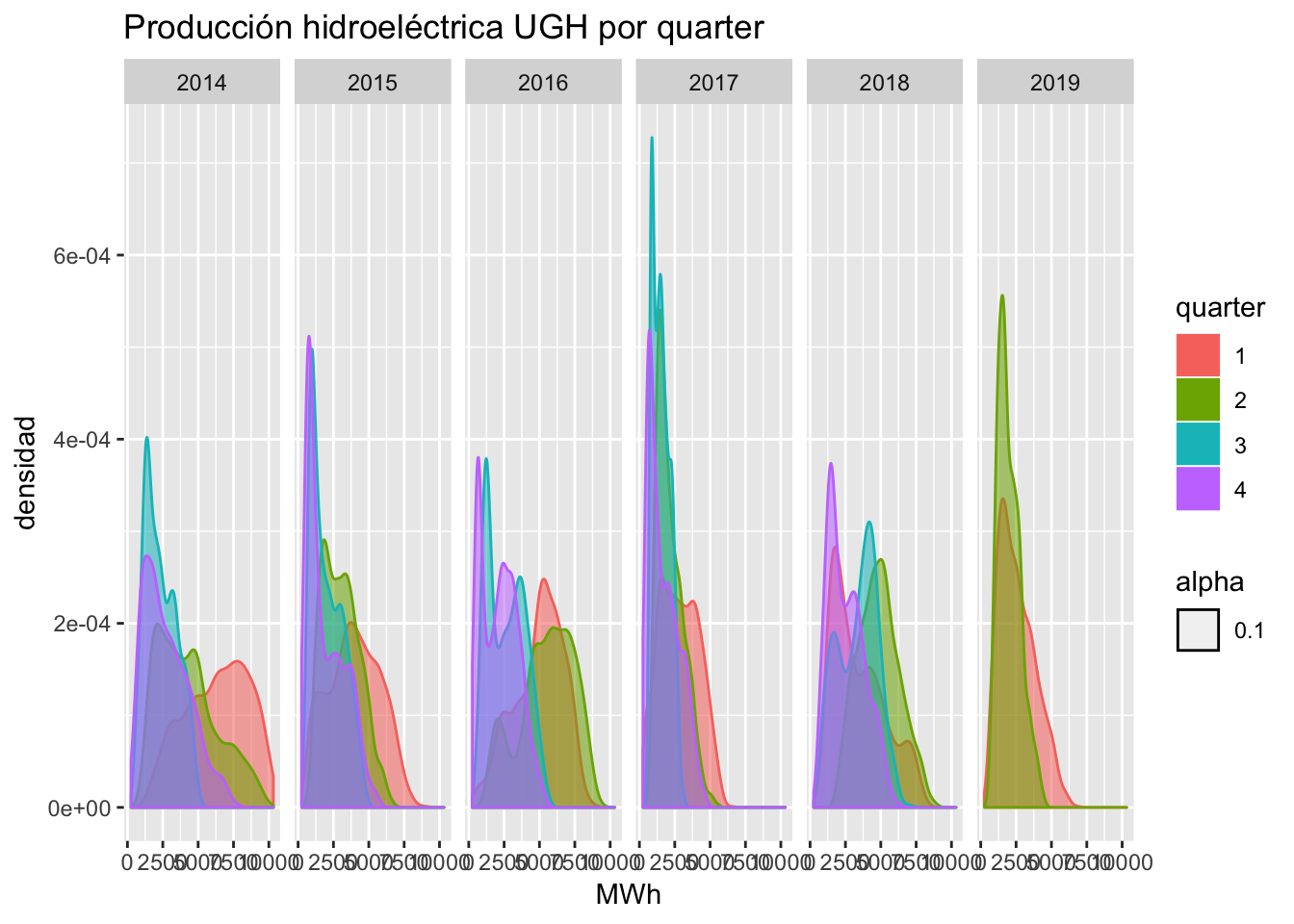
Se observan varios hechos interesantes:
- El año 2014 (muy húmedo) durante el Q1 se produjeron los máximos de generación con medias de 8000 MWh, coincidiendo con el llenado de nuevo de los embalses, que venían ya de niveles altos, fruto de las lluvias del Q4.
- En el año 2015 desaparece dicha producción del Q4, y se apunta el Q1 a niveles de producción cercanos a los 1500 MWh.
- El año 2016 presenta una frecuencia de dos picos: Q1 y Q2 presentan los máximos producidos, y Q3 y Q4 los mínimos.
- El año 2017, anómalo de la swrie, presenta para casi todos los quarters picos de baja producción, excepto para Q1, que aún arrastraba niveles del Q4 de 2016.
- Y finalmente, en lo que llevamos de 2018, con los embalses ya recuperados a partir de Q2, éste y Q3 presentan valores frecuentes mayores a 5000 MWh, pero lejos de los niveles de 2014 o 2016.
Correlación de la energía hidroeléctrica generada y el precio spot
En primer lugar, podría tener algún indicador estadístico que me indicara la intensidad de la correlación y la dirección. Para ello, puedo utilizar la correlación de Pearson, y ver para cada mes de los años 2016, 2017 y 2018, cómo ha evolucionado dicha correlación. Utilizaré el % de cobertura de la UGH sobre la demanda, para dar más peso a los valores que realmente tienen un efecto sobre el precio, ya sea desplazando el punto de casación entre la curva de oferta y de demanda hacia valores más bajos (porque ofertan a precio bajo) o bien haciendo presión alcista sobre el mismo.
# correlación
datos_horarios %>% filter(año %in% c(2014,2015,2016,2017,2018)) %>%
group_by(año, quarter) %>%
do(tidy(cor.test(.$UGH_fraction, .$omie))) %>%
ggplot(aes(x = as.factor(quarter), y = estimate, fill = año)) +
geom_bar(stat="identity", position=position_dodge()) +
ggtitle("Evolución correlación Pearson fracción UGH - precio spot OMIE") +
xlab("quarter") +
ylab("correlación")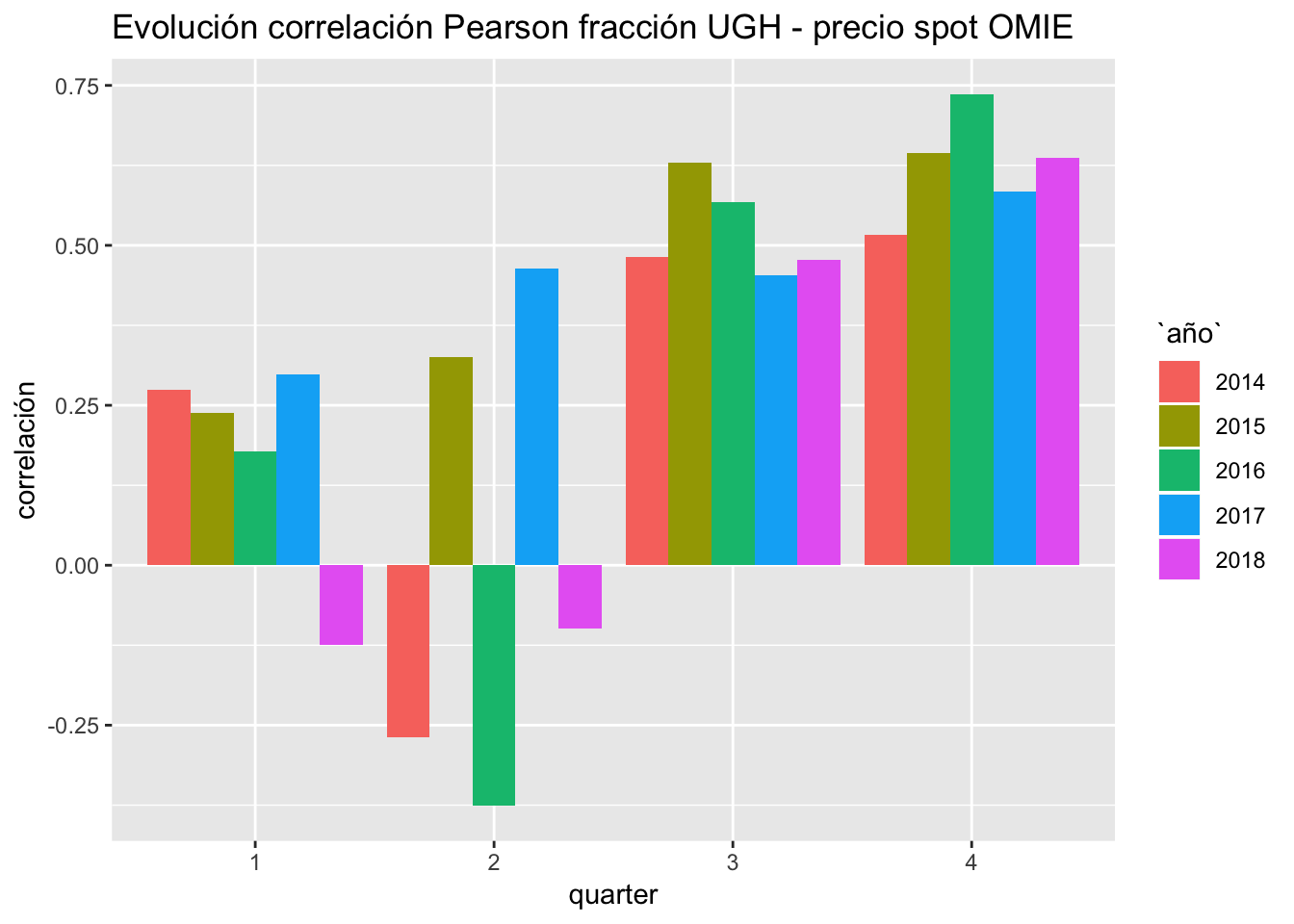
El año 2017 muestra una correlación positiva para todos los quarters, aunque 2018 curiosamente muestra una correlación despreciable durante Q1 y Q2, mostrando ineslaticidad al precio spot.
Todas estas apreciaciones se deben contextualizar con el comportamiento del mercado de cada momento y la tecnología que marca el precio marginal, pero para este análisis básico de exploración de datos, ya resulta suficientemente interesante.
Análisis ANOVA
Aunque gráficamente se puede ver que las medias de la cobertura son diferentes, el análisis de la varianza es una técnica que puede confirmar dicho supuesto o hipótesis.
A continuación realizo el ANOVA para comprobar si el p-valor es suficientemente significativo para rechazar la hipótesis nula y contrastar que las medias anuales por quarter son diferentes:
## Reference: Welch's ANOVA is used as a default. (Delacre, Leys, Mora, & Lakens, PsyArXiv, 2018).Note: Anderson-Darling Normality Test for UGH_fraction : p-value = < 0.001Note: Bartlett's test for homogeneity of variances for factor año : p-value = < 0.001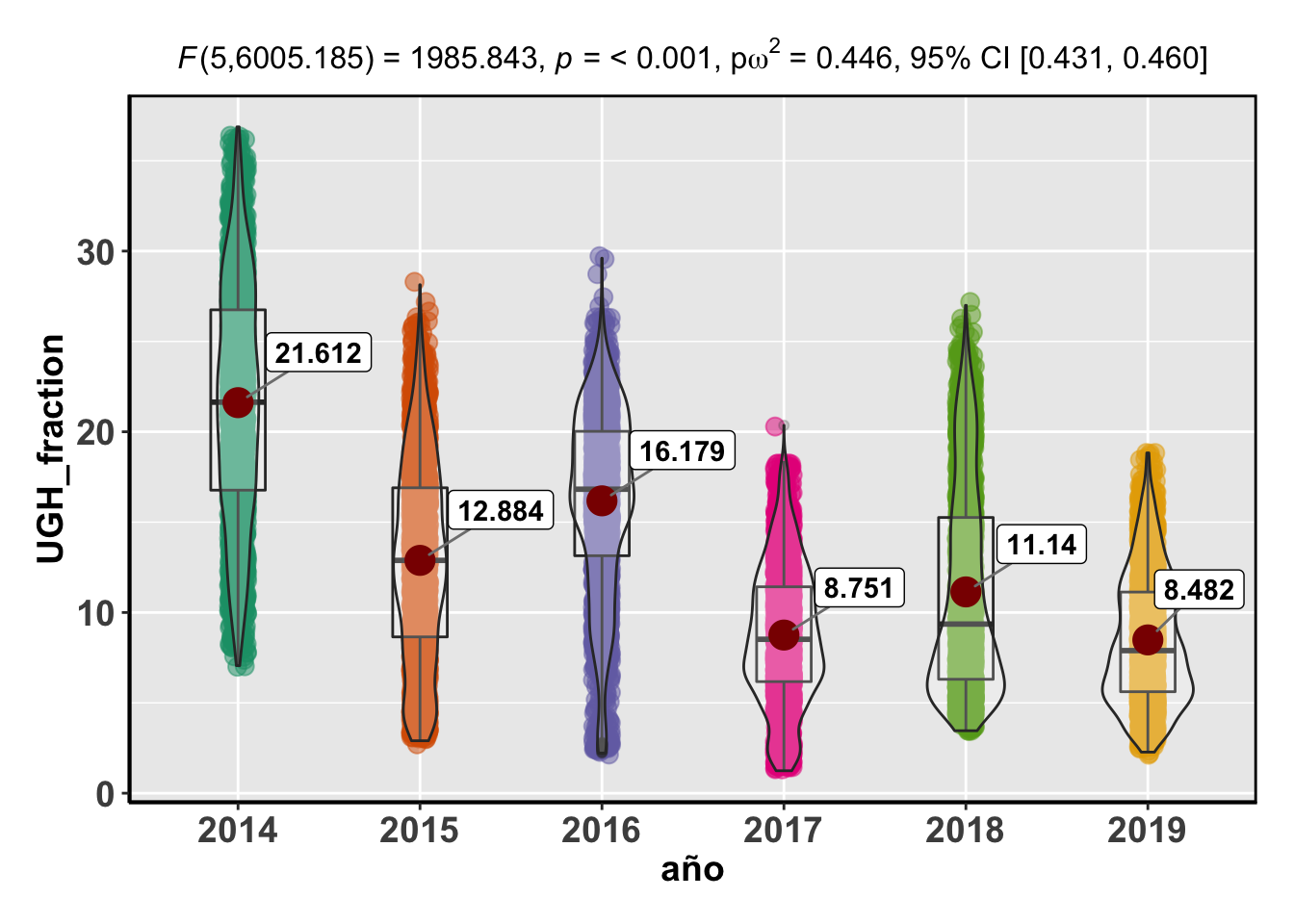
## Df Sum Sq Mean Sq F value Pr(>F)
## año 5 2.023e+10 4.046e+09 1412 <2e-16 ***
## Residuals 12972 3.717e+10 2.866e+06
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Reference: Welch's ANOVA is used as a default. (Delacre, Leys, Mora, & Lakens, PsyArXiv, 2018).Note: Anderson-Darling Normality Test for UGH_fraction : p-value = < 0.001Note: Bartlett's test for homogeneity of variances for factor año : p-value = < 0.001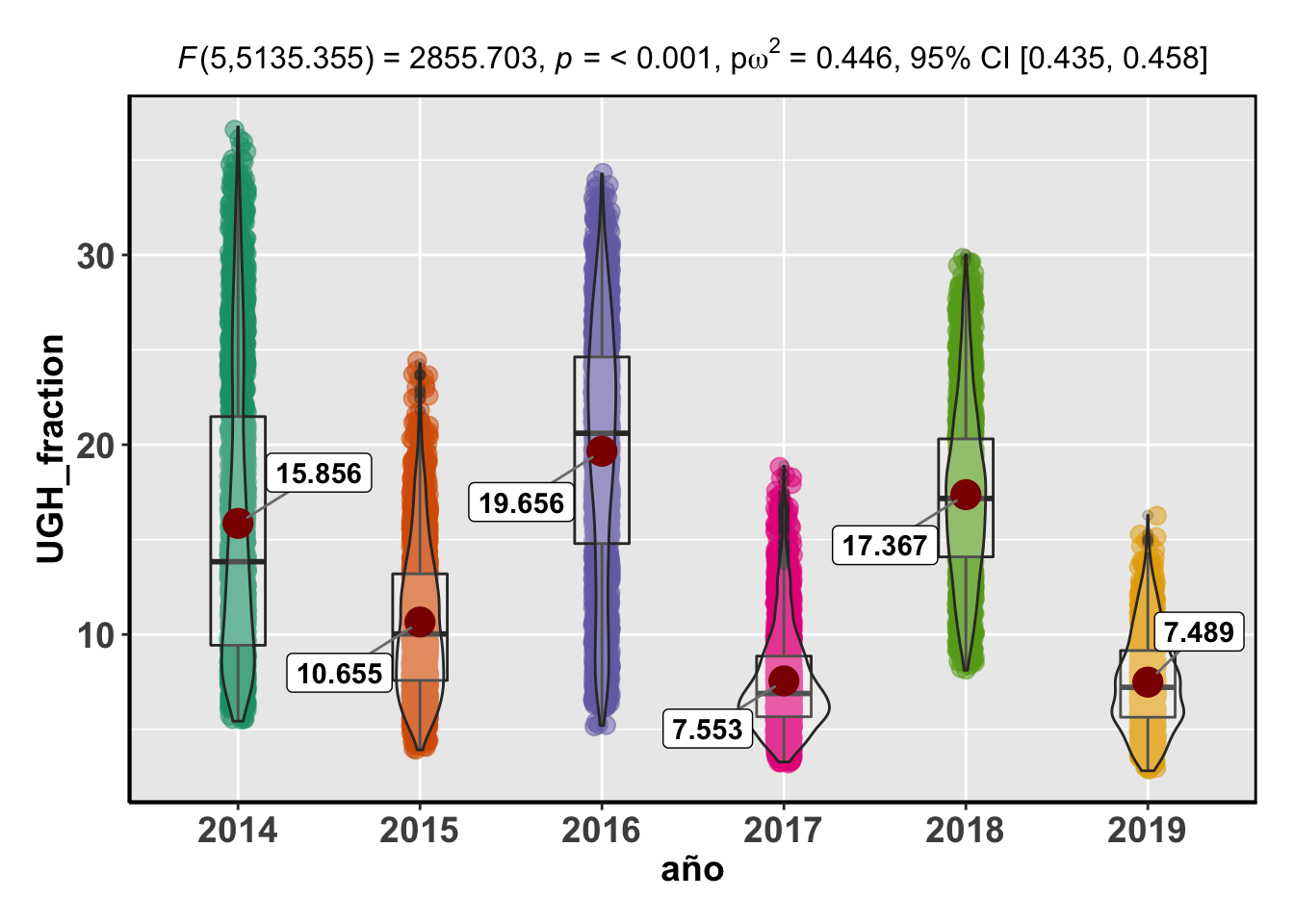
## Df Sum Sq Mean Sq F value Pr(>F)
## año 5 1.786e+10 3.571e+09 1583 <2e-16 ***
## Residuals 11946 2.695e+10 2.256e+06
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Reference: Welch's ANOVA is used as a default. (Delacre, Leys, Mora, & Lakens, PsyArXiv, 2018).Note: Anderson-Darling Normality Test for UGH_fraction : p-value = < 0.001Note: Bartlett's test for homogeneity of variances for factor año : p-value = < 0.001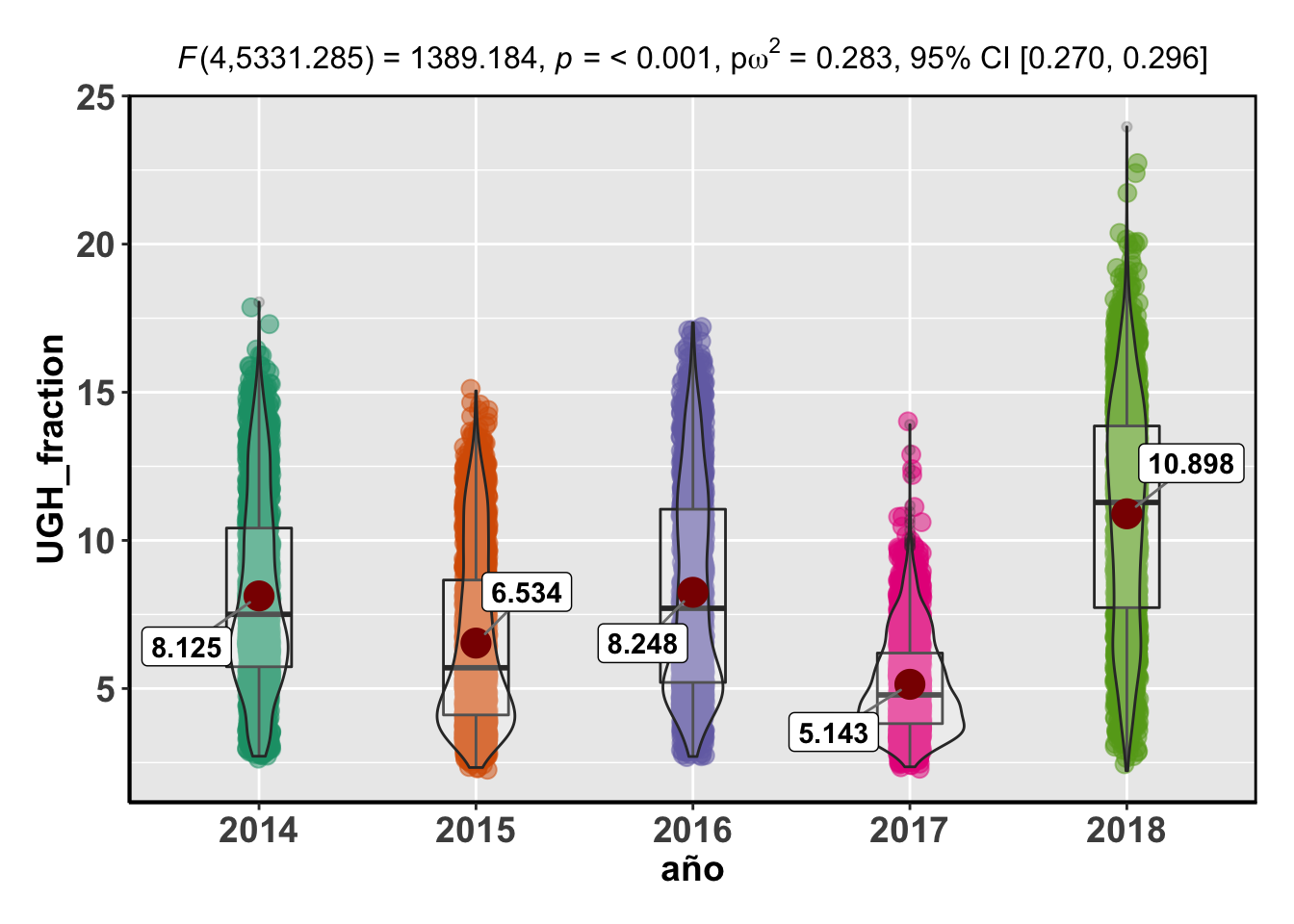
## Df Sum Sq Mean Sq F value Pr(>F)
## año 4 3.366e+09 841448142 713.5 <2e-16 ***
## Residuals 11035 1.301e+10 1179346
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Reference: Welch's ANOVA is used as a default. (Delacre, Leys, Mora, & Lakens, PsyArXiv, 2018).Note: Anderson-Darling Normality Test for UGH_fraction : p-value = < 0.001Note: Bartlett's test for homogeneity of variances for factor año : p-value = < 0.001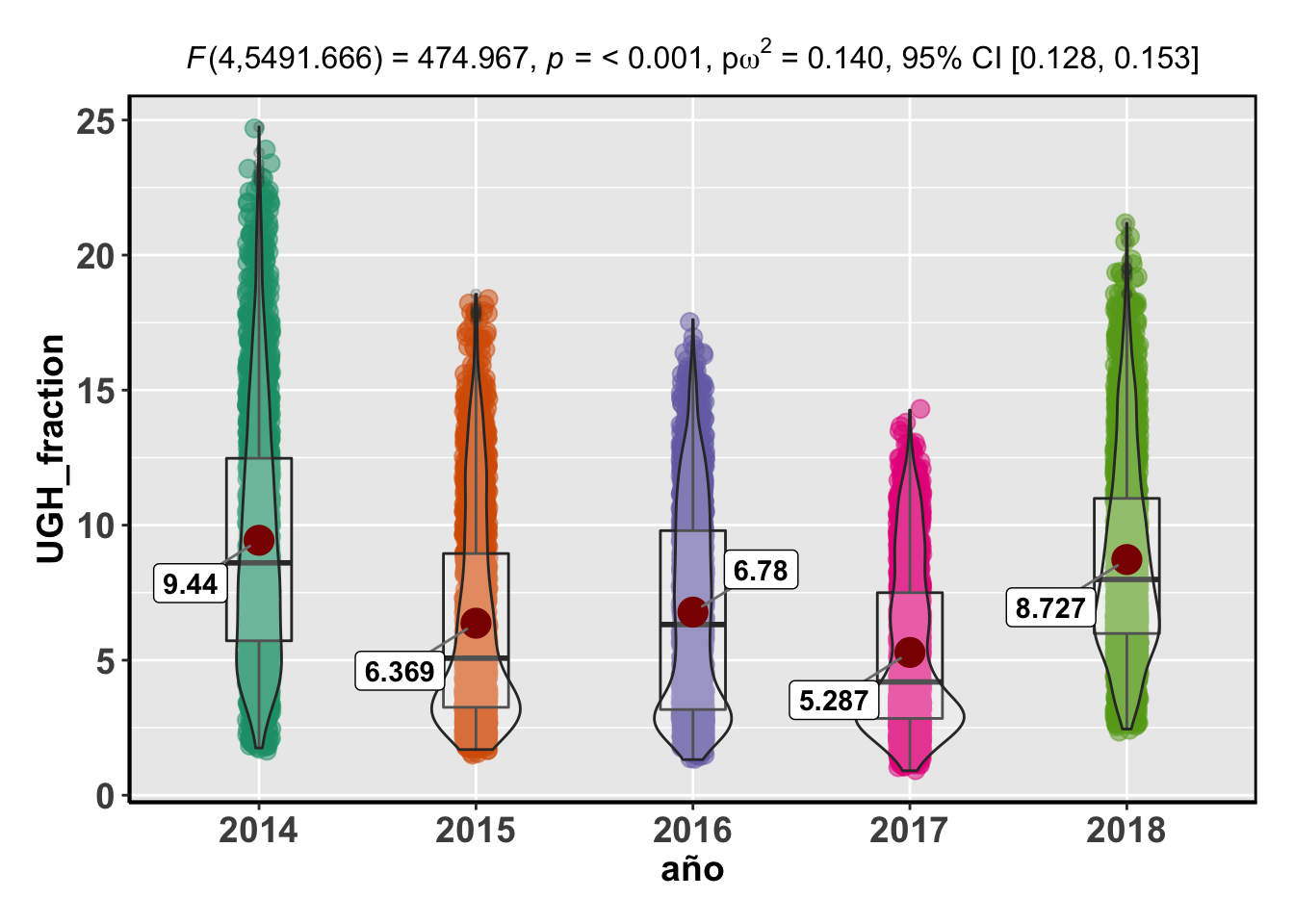
## Df Sum Sq Mean Sq F value Pr(>F)
## año 4 1.727e+09 431733867 273.6 <2e-16 ***
## Residuals 11035 1.741e+10 1577897
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Obviamente, todos los p-valores son significativos, confirmando que estadísticamente, existen diferencias de cobertura de la UGH entre los años estudiados para cada uno de los quarter.
Evolución de interacción precio spot - cobertura UGH
Los siguientes gráficos muestran el % de UGH que cubre la demanda programada para cada hora, agrupados por quarters y mes y manteniendo sólo los días laborables, con el objetivo de intentar homogeneizar el análisis:
Comparativa anual para el Q1
datos_horarios %>% filter(año %in% c(2014, 2015, 2016, 2017, 2018), quarter == 1, tipo == "L") %>%
ggplot(aes(x=UGH_fraction, y=omie, color = as.factor(año))) +
geom_point(aes(alpha = 0.1)) +
geom_smooth(method = "loess") +
facet_grid(mes ~ .) +
ggtitle("Cobertura UGH vs omie para el Q1")
Se confirma que para el Q1, enero fue un mes en el que a mayor % de UGH, mayor precio spot. Esto no contesta la pregunta de si la UGH tuvo un efecto de contención o no (es decir, ¿pudo haber sido más caro de no ser por la UGH?. Tampoco es la pregunta que me estoy haciendo). Febrero sí que presenta para el año 2014 una disminución leve del precio spot a mayor % de cobertura. Y finalmente marzo tuvo un abanico de cobertura muy amplio, excepto claro está, para 2017, donde las plantas no tenían con qué producir.
Comparativa anual para el Q2
datos_horarios %>% filter(año %in% c(2014, 2015, 2016, 2017, 2018), quarter == 2, tipo == "L") %>%
ggplot(aes(x=UGH_fraction, y=omie, color = as.factor(año))) + geom_point(aes(alpha = 0.1)) +
geom_smooth(method = "loess") +
facet_grid(mes ~ .) +
ggtitle("Cobertura UGH vs omie para el Q2")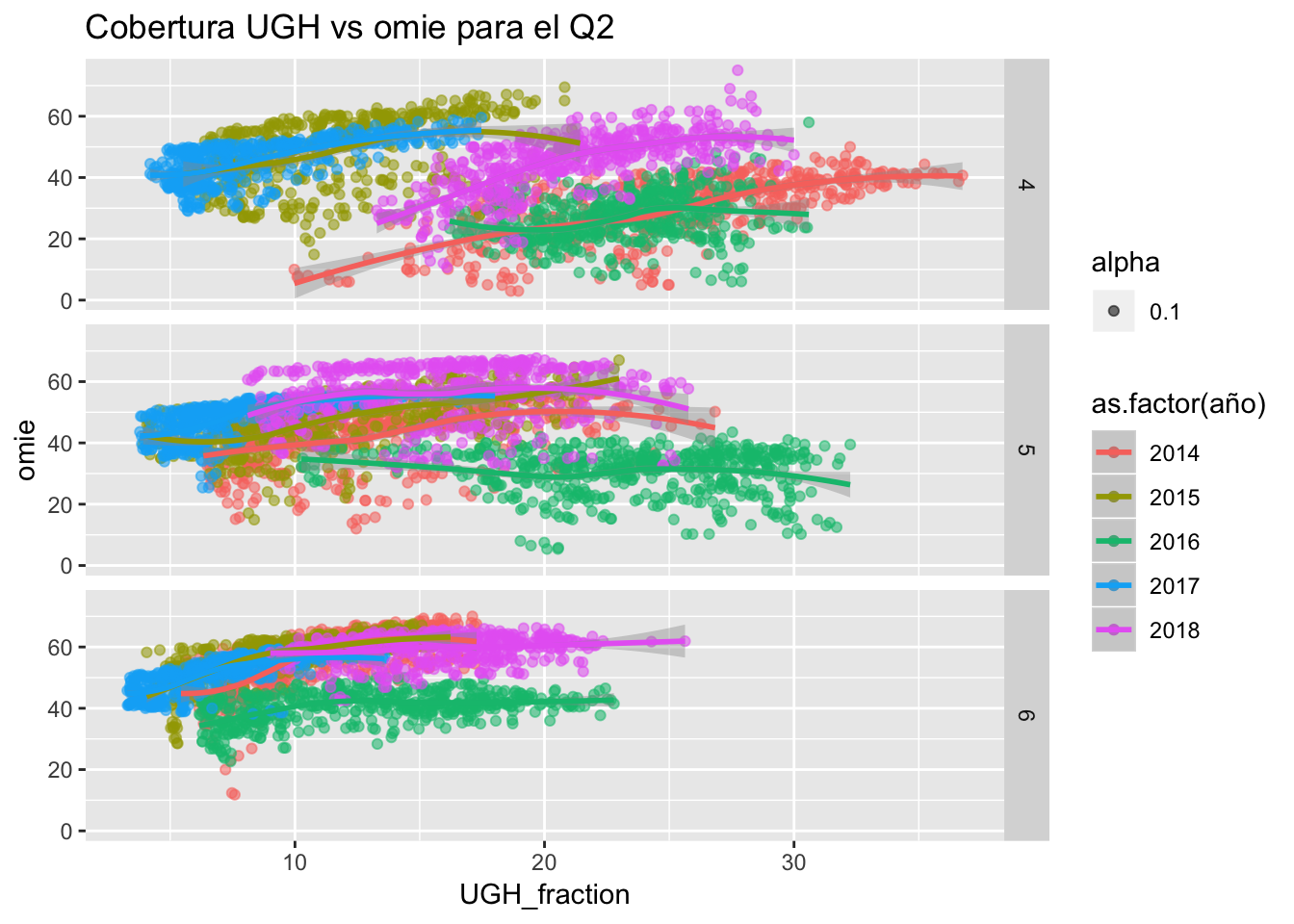
Para el Q2 se empieza a ver algo claro un efecto diferenciador del comportacmiento en 2018: abril fue un mes donde el comportamiento fue muy parecido entre 2015 y 2017 (siendo muy diferentes a nivel de reservas) y entre 2014 y 2016. El año 2018 se sitúa justo en medio de ambos pares. Para los meses de mayo y junio, el nivel de precios de 2018 se sitúa por encima del resto. Destaca por otra parte el año 2016, donde la UGH fue inelástica al precio o incluso deprimió éste.
Comparativa anual para el Q3
datos_horarios %>% filter(año %in% c(2014, 2015, 2016, 2017, 2018), quarter == 3, tipo == "L") %>%
ggplot(aes(x=UGH_fraction, y=omie, color = as.factor(año))) +
geom_point(aes(alpha = 0.1)) +
geom_smooth(method = "loess") +
facet_grid(mes ~ .) +
ggtitle("Cobertura UGH vs omie para el Q3")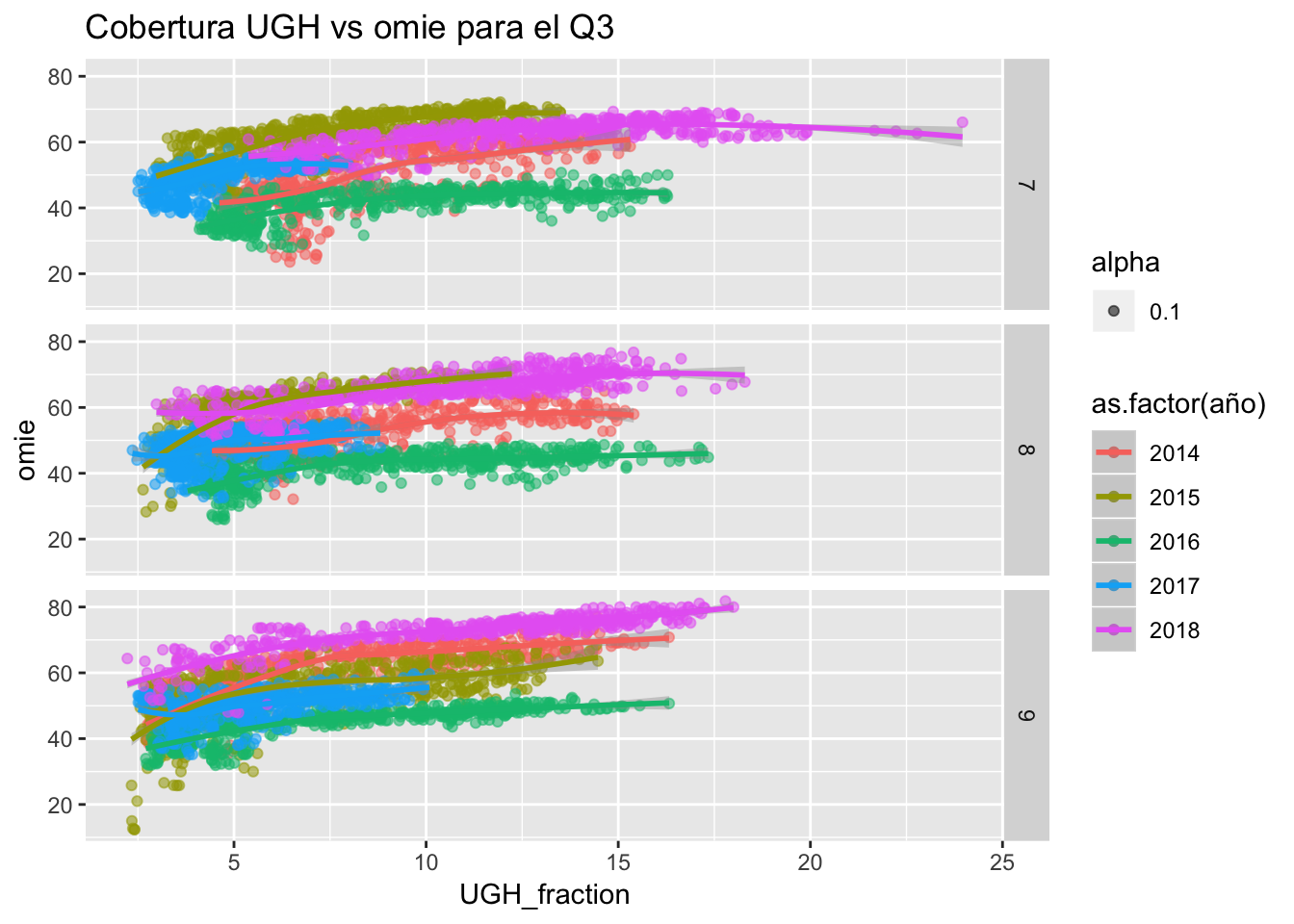
Para el Q3, cabe destacar el amplio rango de cobertura que tuvo durante el presente año esta tecnología, aunque a nivel de precios se mantuvo parecido a 2015, y por encima del año seco.
Comparativa anual para el Q4
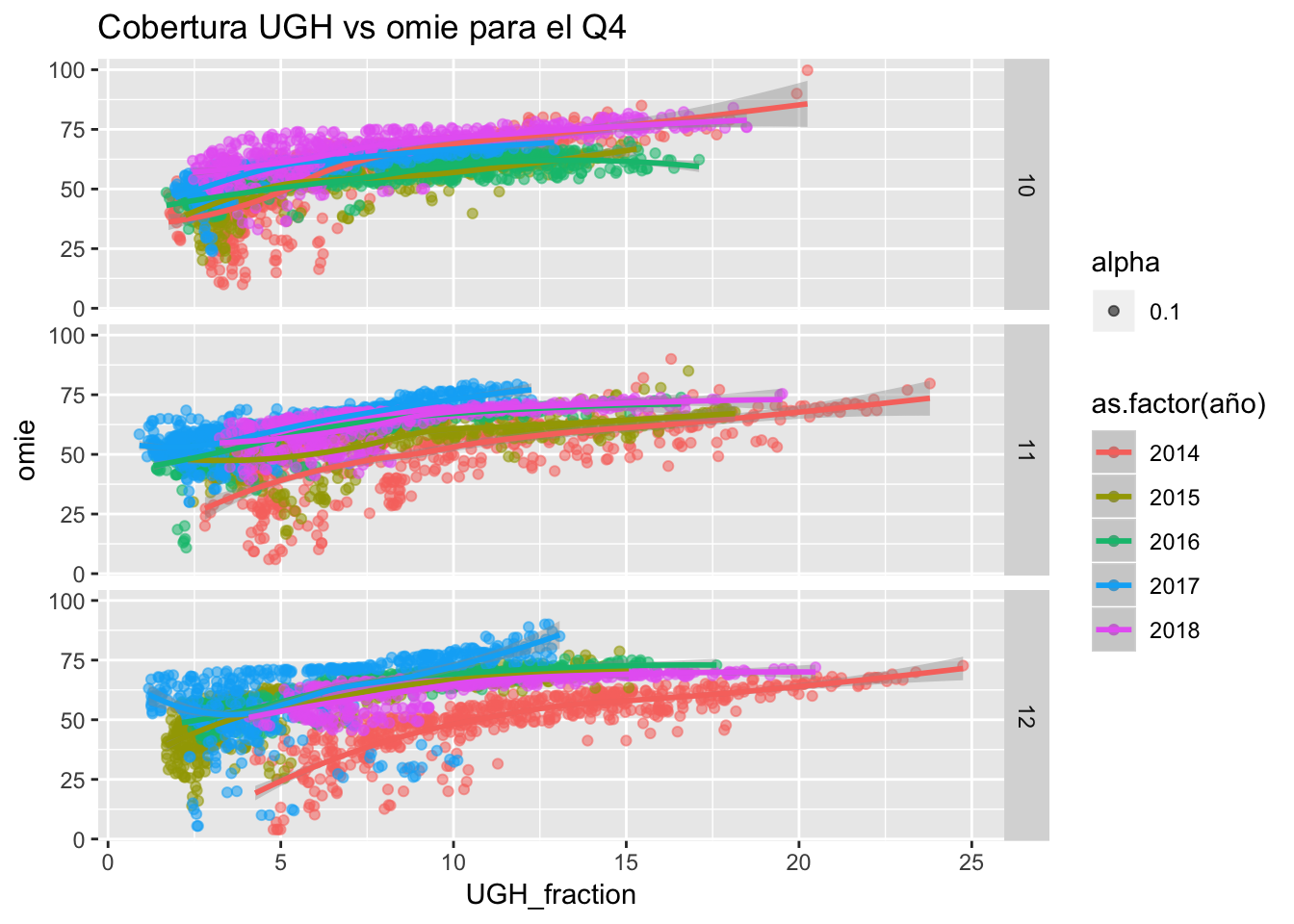
Aún no se disponen de datos del Q4 del presente año, pero se puede avanzar que con rango de cobertura pequeño, 2017 marcó el nivel de precios más elevado de la serie.
Evolución de la correlación entre precio spot, nivel de reservas generación UGH con valores horarios
Ciertamente, para hallar explicación a la correlación entre precio, reservas y producción, es necesario graficar dicha interacción visual de alguna manera. Utilizaré un diagrama de dispersión donde la tercera variable o eje será el nivel de reservas, indicando con color azul más claro un nivel alto de energía embalsada, y en oscuro un nivel bajo:
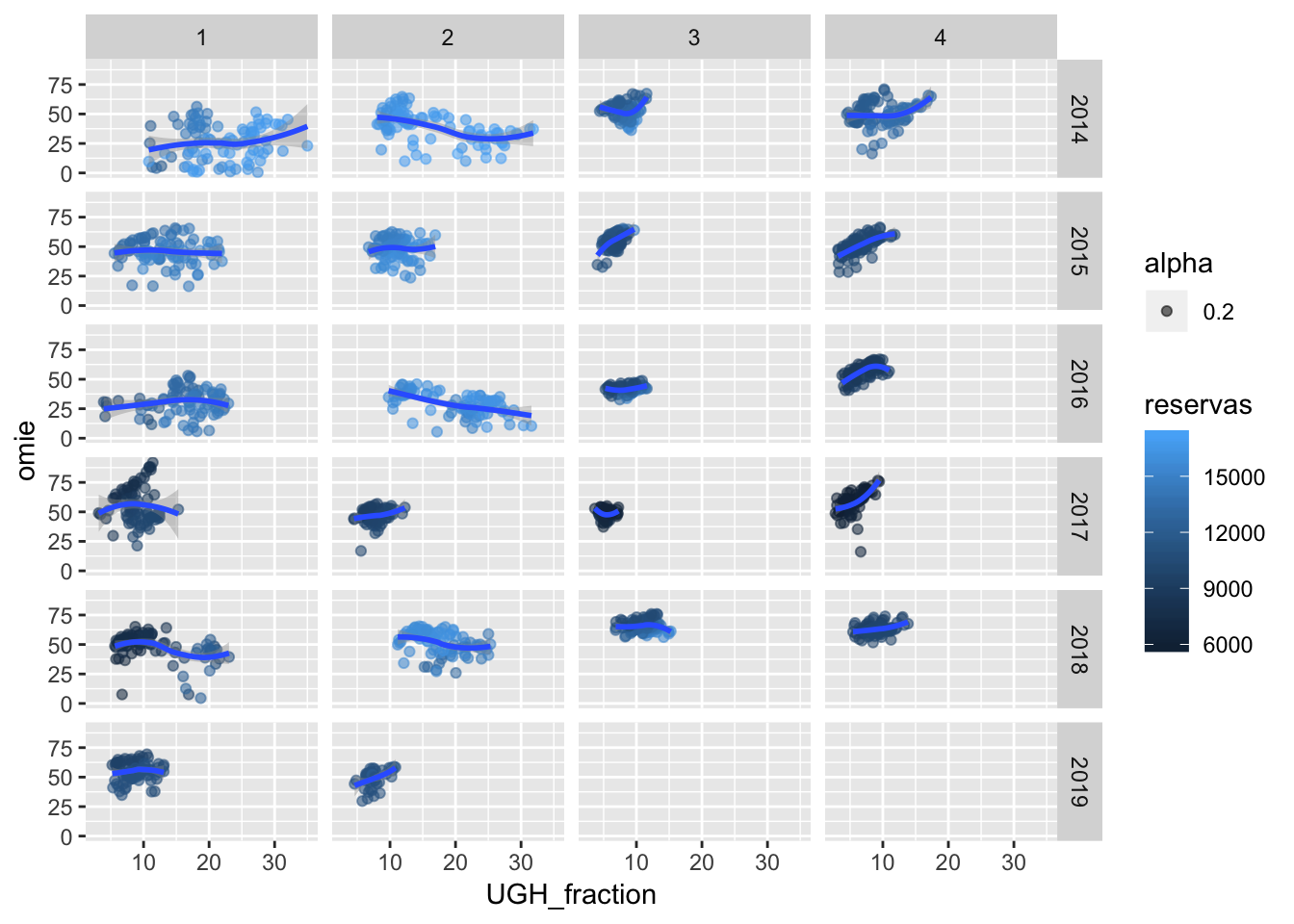
Salta a la vista que en años y quarters donde los puntos son claros la función loess aplicada muestra una relación inversamente proporcional entre el precio spot y la generación UGH. Esto también se cumple para el año 2017, donde a medida que se generaba más, el precio spot se encarecía (si bien es cierto que la función loess parece algo caprichosa para el Q1, donde los datos muestran una dispersión en dos direcciones, alcista y bajista).
Sin embargo, el año 2018 no sigue estos patrones a primera vista: el Q2, con un nivel de llenado similar a 2014, 2015 y 2016, muestra una tendencia casi plana, en lugar de depresora. En lo que llevamos de Q3, sin embargo, parece inelástico, en lugar de alcista, aunque también es cierto que el nivel de cobertura es el mayor de toda la serie de datos para dicho Q.
Análisis por clusterización mediante k-medias
La clusterización por k-medias (o k-means) es una técnica exploratoria que permite agrupar mediante distancias las observaciones de un gran conjunto de datos, buscando la máxima homogeneidad para cada cluster o grupo. Dado que tengo 5 años de datos, filtraré por un mes en concreto y aplicaré el algoritmo para que trate de clasificar cada par de valores precio spot-cobertura de UGH en cada uno de los 5 años:
# Función para convertir dataframe a matriz y conservar las fechas
matrix.please<-function(x) {
m<-as.matrix(x[,-1])
rownames(m)<-as.character(x[,1])
m
}
# Preparamos matriz para los meses de mayo
data_to_matrix <- datos_diarios %>% filter(mes == 5) %>%
select(fecha, omie, UGH_fraction, reservas) %>%
as.data.frame() %>%
unique()
data_to_cluster <- matrix.please(data_to_matrix) %>% scale() %>% unique()
# Creación de los clústeres
set.seed(1)
km.res <- kmeans(data_to_cluster, 5, nstart = 100)
# Gráfico
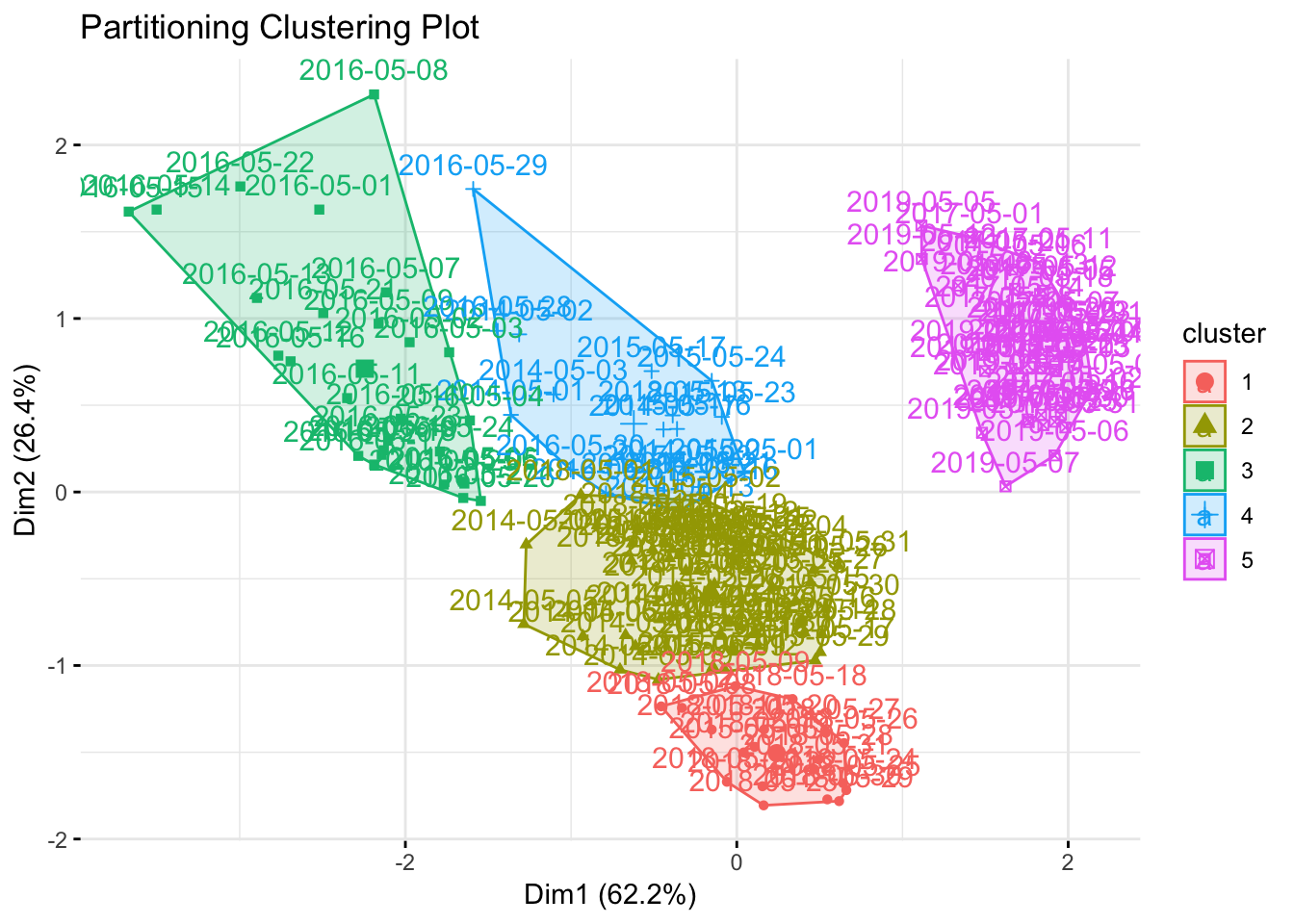
fviz_cluster(km.res, data = data_to_cluster,
ggtheme = theme_minimal(),
main = "Partitioning Clustering Plot"
)
# Tabla de la clasificación cluster
km.res$cluster %>% tidy() %>%
separate(col = names, sep = "-", into = c("año", "mes", "dia")) %>%
select(x, año, mes) %>%
table()## , , mes = 05
##
## año
## x 2014 2015 2016 2017 2018 2019
## 1 0 1 0 0 18 0
## 2 23 23 0 0 12 0
## 3 0 0 27 0 0 0
## 4 8 7 4 0 1 0
## 5 0 0 0 31 0 13He escogido mayo por ser un mes donde se esperan ver de forma notoria las diferencias con respecto a años anteriores, y es interesante ver que 18 días de mayo son clasificados como cluster nº 1, donde también se cuela un día de 2015. Pero hay otros 12 días clasificados bajo el cluster nº 5, donde mayoritariamente también están casi la totalidad de los días de 2014 y 2015. La propia tabla ya dice que es el único año donde tenemos una dicotomía de comportamiento, de ahí que recaiga en 2 clusters.
Finalmente, para recapitular la información, se compara con un diagrama de cajas tanto la cobertura de UGH como el precio OMIE:

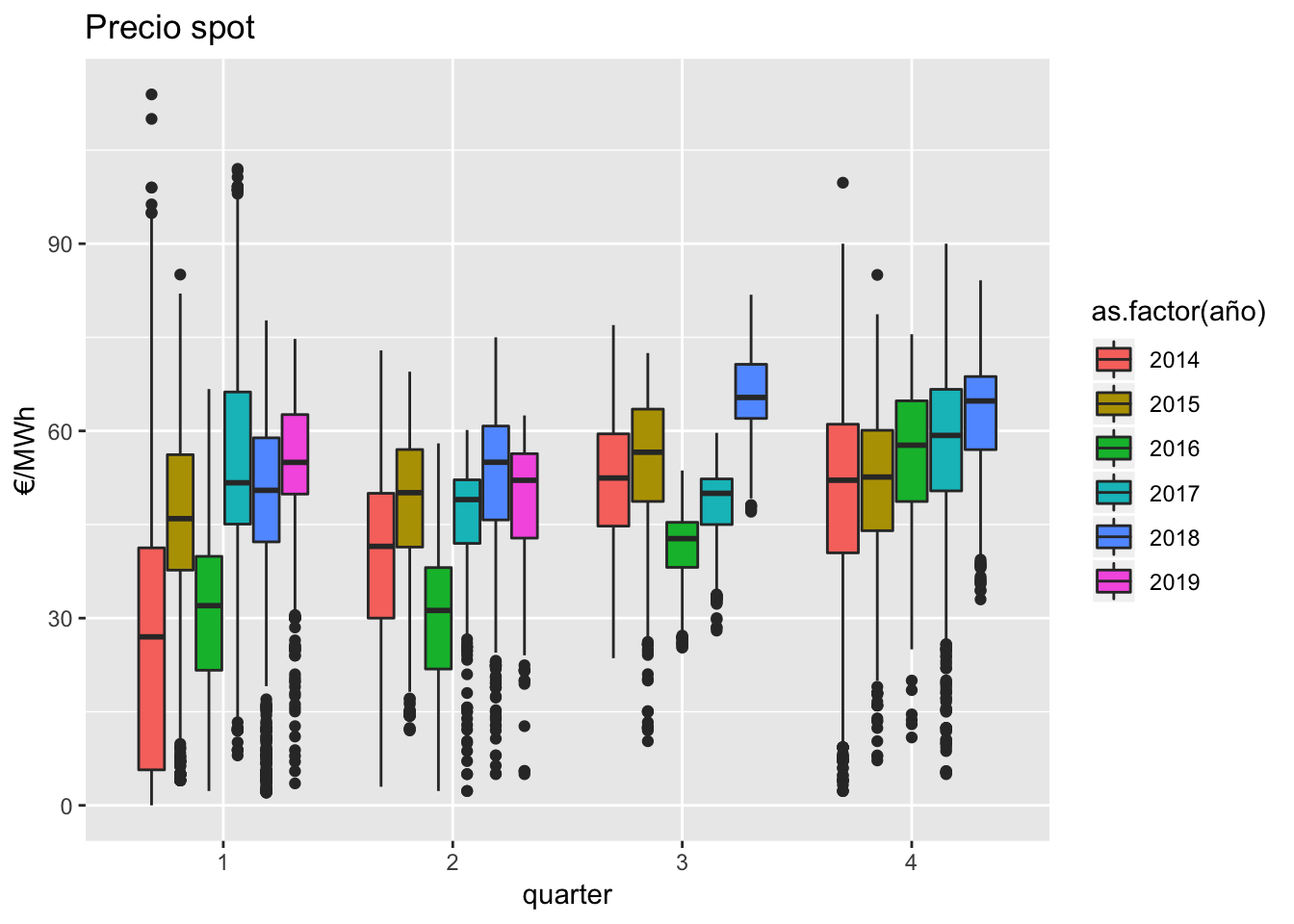
Conclusiones
El año 2018 se está caracterizando por unos precios de omie con medias aritméticas elevadas en los 3 quarters hasta donde se disponen datos, pero es el en Q2 donde, con una cobertura hidroeléctrica superada sólo por el año 2016 (año muy húmedo), el precio marca un máximo de la serie. Estas conclusiones van en línea con el hecho de que la UGH está marcando precio marginal para la mayoría de las horas en los últimos meses, según la propia OMIE:
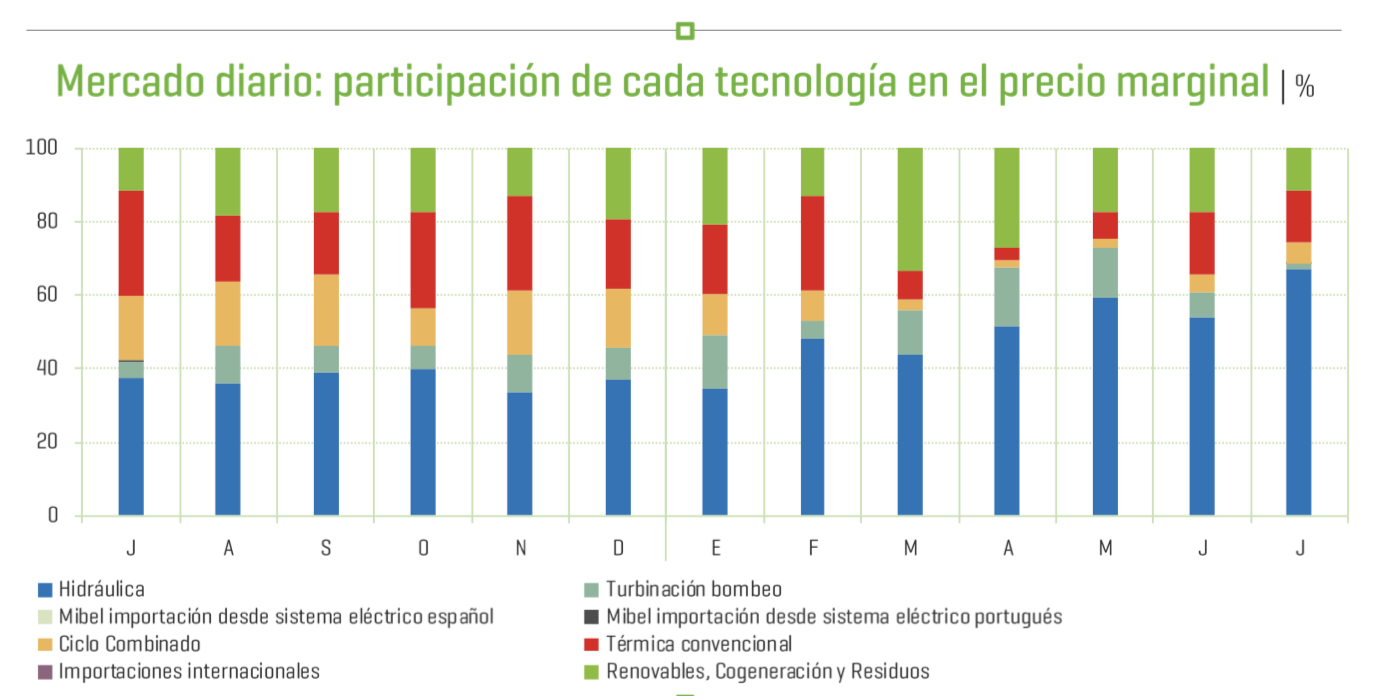
Imagen del Boletín REE Julio 2018.